题目内容
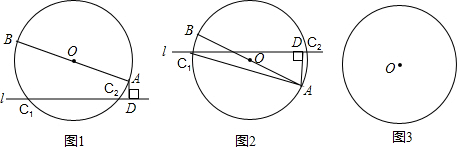
如图①,AB是⊙O的直径,AC是弦,直线EF和⊙O相切于点C,AD⊥EF,垂足为D.
(1)求证:∠DAC=∠BAC;
(2)若把直线EF向上平行移动,如图②,EF交⊙O于G、C两点,若题中的其它条件不变,猜想:此时与∠DAC相等的角是哪一个?并证明你的结论.

(1)求证:∠DAC=∠BAC;
(2)若把直线EF向上平行移动,如图②,EF交⊙O于G、C两点,若题中的其它条件不变,猜想:此时与∠DAC相等的角是哪一个?并证明你的结论.

分析:(1)连接BC,OC,由半径OC=OA,根据等边对等角可得出一对角相等,再由OC与AD都与EF垂直,得到OC与AD平行,根据两直线平行内错角相等可得一对内错角相等,等量代换可得出∠DAC=∠BAC,得证;
(2)∠BAG=∠CAD,理由如下:连接BC,由AB为圆O的直径,根据直径所对的圆周角为直角可得出∠BCA为直角,即三角形ABC为直角三角形,根据直角三角形中的两个锐角互余可得出一对角互余,由AD垂直于EF,可得出三角形AGD为直角三角形,同理得到一对锐角互余,再由同弧所对的圆周角相等可得出∠B与∠AGD相等,进而确定出∠BAG=∠GAD,等式两边都减去∠CAG即可得到∠BAC=∠GAD,得证.
(2)∠BAG=∠CAD,理由如下:连接BC,由AB为圆O的直径,根据直径所对的圆周角为直角可得出∠BCA为直角,即三角形ABC为直角三角形,根据直角三角形中的两个锐角互余可得出一对角互余,由AD垂直于EF,可得出三角形AGD为直角三角形,同理得到一对锐角互余,再由同弧所对的圆周角相等可得出∠B与∠AGD相等,进而确定出∠BAG=∠GAD,等式两边都减去∠CAG即可得到∠BAC=∠GAD,得证.
解答:
解:(1)连接OC,如图①所示,
∵OC=OA,
∴∠BAC=∠OCA,
∵EF切⊙O于C,
∴OC⊥EF,又AD⊥EF,
∴OC∥AD,
∴∠OCA=∠DAC,
∴∠DAC=∠BAC;
(2)∠BAG=∠DAC,理由如下:
连接BC,如图②所示,
∵AB为⊙O的直径,
∴∠BCA=90°,
∴∠B+∠BAC=90°,
∵AD⊥EF,∴∠ADG=90°,
∴∠AGD+∠GAD=90°,
又
=
,∴∠B=∠AGD,
∴∠BAC=∠GAD,
∴∠BAG+∠GAC=∠GAC+∠DAC,即∠BAG=∠DAC.

解:(1)连接OC,如图①所示,
∵OC=OA,
∴∠BAC=∠OCA,
∵EF切⊙O于C,
∴OC⊥EF,又AD⊥EF,
∴OC∥AD,
∴∠OCA=∠DAC,
∴∠DAC=∠BAC;
(2)∠BAG=∠DAC,理由如下:
连接BC,如图②所示,
∵AB为⊙O的直径,
∴∠BCA=90°,
∴∠B+∠BAC=90°,
∵AD⊥EF,∴∠ADG=90°,
∴∠AGD+∠GAD=90°,
又
 |
| AC |
 |
| AC |
∴∠BAC=∠GAD,
∴∠BAG+∠GAC=∠GAC+∠DAC,即∠BAG=∠DAC.
点评:此题考查了切线的性质,等腰三角形的性质,平行线的性质,圆周角定理,利用了等量代换及转化的思想,连接出相应的辅助线,灵活运用性质及定理是解本题的关键.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目

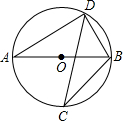 如图,若AB是⊙0的直径,CD是⊙O的弦,∠C=30°,BD=1,则⊙O的半径是( )
如图,若AB是⊙0的直径,CD是⊙O的弦,∠C=30°,BD=1,则⊙O的半径是( ) (2013•海沧区一模)如图,若AB是⊙O的直径,CD是⊙O的弦,∠ABD=50°,则∠BCD=
(2013•海沧区一模)如图,若AB是⊙O的直径,CD是⊙O的弦,∠ABD=50°,则∠BCD=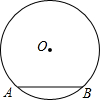 如图,弦AB是⊙O的内接正方形的一条边,则弦AB所对的圆周角的度数为
如图,弦AB是⊙O的内接正方形的一条边,则弦AB所对的圆周角的度数为