题目内容
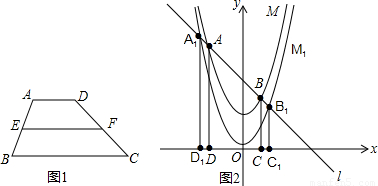
若梯形两底中点的连线长为d，两腰的长分别为a．b，则d与a+b的大小关系是________．
d＜
分析：根据题意画出图形，过E分别作AB、CD的平行线EG、EH，延长EF至N，使FN=EF，根据全等三角形的判定定理可知△GNF≌△HEF，再由三角形的三边关系即可求解．
解答：
解：如图所示，过E分别作AB、CD的平行线EG、EH，延长EF至N，使FN=EF，连接NG，
∵AE∥BC，AB∥EG，
∴四边形ABGE是平行四边形，AE=BG，AB=EG，
同理可知BG=HC，CD=EH，
∵E、F分别是AD、BC的中点，
∴AE=ED，BF=FC，
∴GF=FH，
∵EF=FN，∠GFN=∠EFC，
∴△GNF≌△HEF，
EH=CD=GN，
在△EGN中，由三角形的三边关系可知EN＜EG+NG，即2d＜a+b，故d＜．
点评：此题比较复杂，解答此题的关键是作出辅助线，利用三角形的三边关系求解．
分析：根据题意画出图形，过E分别作AB、CD的平行线EG、EH，延长EF至N，使FN=EF，根据全等三角形的判定定理可知△GNF≌△HEF，再由三角形的三边关系即可求解．
解答：
解：如图所示，过E分别作AB、CD的平行线EG、EH，延长EF至N，使FN=EF，连接NG，∵AE∥BC，AB∥EG，
∴四边形ABGE是平行四边形，AE=BG，AB=EG，
同理可知BG=HC，CD=EH，
∵E、F分别是AD、BC的中点，
∴AE=ED，BF=FC，
∴GF=FH，
∵EF=FN，∠GFN=∠EFC，
∴△GNF≌△HEF，
EH=CD=GN，
在△EGN中，由三角形的三边关系可知EN＜EG+NG，即2d＜a+b，故d＜
．点评：此题比较复杂，解答此题的关键是作出辅助线，利用三角形的三边关系求解．
练习册系列答案
全能测控期末小状元系列答案
智趣暑假温故知新系列答案
相关题目
（AD+BC）利用上面的知识，完成下面题目的解答已知：直线l与抛物线M交于点A，B两点，抛物线M的对称轴为y轴，过点A，B作x轴的垂线段，垂足分别为D，C，已知A（-1，3），B（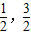
）