题目内容
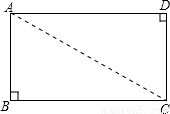
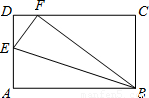 如图,矩形纸片ABCD中,AB=5,BC=3,点E在AD边上,将纸片沿BE折叠,使点A落在CD边上的F处.下列结论中:
如图,矩形纸片ABCD中,AB=5,BC=3,点E在AD边上,将纸片沿BE折叠,使点A落在CD边上的F处.下列结论中:①DE=
 ;②tan∠EBF=
;②tan∠EBF= ;③四边形ABFE的面积是矩形ABCD的面积的一半;④若在折痕BE上有点Q,使得△BFQ为等腰三角形,则EQ必然为
;③四边形ABFE的面积是矩形ABCD的面积的一半;④若在折痕BE上有点Q,使得△BFQ为等腰三角形,则EQ必然为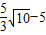 ;⑤若在折痕BE上有点P到边CD的距离与到点A的距离相等,则此相等距离为1.8.以上结论一定正确的个数为( )
;⑤若在折痕BE上有点P到边CD的距离与到点A的距离相等,则此相等距离为1.8.以上结论一定正确的个数为( )A.2个
B.3个
C.4个
D.5个
【答案】分析:首先计算出CF的长,再在△DEF中用勾股定理即可算出DE的长,进而判断出①的正误;根据①中计算的DE的长,可以表示出EF和AE的长,进而可以表示出tan∠EBF,可判断出②的正误;根据前面计算的AE长,计算出四边形ABFE的面积,再计算出矩形ABCD的面积,可判断出③的正误;在折痕BE上有点Q,使得△BFQ为等腰三角形可有两种情况,一种情况一定错误;再由翻折变换的性质得出F、A′重合,分别延长BE,DC相交于点G,由平行线的性质可得出GA′=BA′=AB=5,再根据相似三角形的判定定理得出△BCG∽△PA′G,求出其相似比,进而可求出答案.
解答: 解:∵四边形ABCD是矩形,
解:∵四边形ABCD是矩形,
∴DC=AB=5,AD=BC=3,
根据折叠可得BF=AB=5,
在Rt△BFC中:FC= =
= =4,
=4,
则DF=5-4=1,
设DE=x,则AE=EF=3-x,
12+x2=(3-x)2,
解得:x= ,故①正确;
,故①正确;
∵ED= ,AD=3,
,AD=3,
∴AD=EF=3- =
= ,
,
tan∠EBF= =
= =
= ,故②正确;
,故②正确;
根据折叠可得四边形ABFE的面积=2S△ABE=2× ×AB×AE=2×
×AB×AE=2× ×5×
×5× =
= ,
,
是矩形ABCD的面积=3×5=15,
故③错误;
在折痕BE上有点Q,使得△BFQ为等腰三角形可有两种情况:
一种是BF=BQ,另一种是QF=QB,
故④错误;
如图所示,设PF⊥CD,
∵AP=FP,
由翻折变换的性质可得AP=A′P,
∴FP=A′P,
∴FP⊥CD,
∴A′,F,P三点构不成三角形,
∴F,A′重合分别延长BE,DC相交于点G,
∵AB平行于CD,
∴∠ABG=∠BGC,
∵∠ABG=∠A′BG,BGD=∠A′BG,
∴GA′=BA′=AB=5,
∵PA′(PF)⊥CD,
∴PA′∥BC,
∴△BCG∽△PA′G,
∵Rt△BCA′中,BA′=5,BC=3,
∴CA′=4,CG=CA′+A′G=3+5=9,
∴△BCG与△PA′G的相似比为9:5,
∴BC:PA′=9:5,
∵BC=3,
∴PA′= ,即相等距离为
,即相等距离为 ,故⑤错误.
,故⑤错误.
故正确的有2个.
故选:A.
点评:本题考查了图形翻折变换的性质及相似三角形的判定与性质,根据题意画出图形,作出辅助线,利用数形结合求解是解答此题的关键.
解答:
 解:∵四边形ABCD是矩形,
解:∵四边形ABCD是矩形,∴DC=AB=5,AD=BC=3,
根据折叠可得BF=AB=5,
在Rt△BFC中:FC=
 =
= =4,
=4,则DF=5-4=1,
设DE=x,则AE=EF=3-x,
12+x2=(3-x)2,
解得:x=
 ,故①正确;
,故①正确;∵ED=
 ,AD=3,
,AD=3,∴AD=EF=3-
 =
= ,
,tan∠EBF=
 =
= =
= ,故②正确;
,故②正确;根据折叠可得四边形ABFE的面积=2S△ABE=2×
 ×AB×AE=2×
×AB×AE=2× ×5×
×5× =
= ,
,是矩形ABCD的面积=3×5=15,
故③错误;
在折痕BE上有点Q,使得△BFQ为等腰三角形可有两种情况:
一种是BF=BQ,另一种是QF=QB,
故④错误;
如图所示,设PF⊥CD,
∵AP=FP,
由翻折变换的性质可得AP=A′P,
∴FP=A′P,
∴FP⊥CD,
∴A′,F,P三点构不成三角形,
∴F,A′重合分别延长BE,DC相交于点G,
∵AB平行于CD,
∴∠ABG=∠BGC,
∵∠ABG=∠A′BG,BGD=∠A′BG,
∴GA′=BA′=AB=5,

∵PA′(PF)⊥CD,
∴PA′∥BC,
∴△BCG∽△PA′G,
∵Rt△BCA′中,BA′=5,BC=3,
∴CA′=4,CG=CA′+A′G=3+5=9,
∴△BCG与△PA′G的相似比为9:5,
∴BC:PA′=9:5,
∵BC=3,
∴PA′=
 ,即相等距离为
,即相等距离为 ,故⑤错误.
,故⑤错误.故正确的有2个.
故选:A.
点评:本题考查了图形翻折变换的性质及相似三角形的判定与性质,根据题意画出图形,作出辅助线,利用数形结合求解是解答此题的关键.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
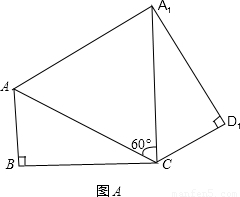
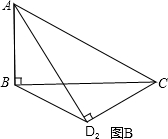
 如图,矩形纸片ABCD中,AB=4,BC=4
如图,矩形纸片ABCD中,AB=4,BC=4

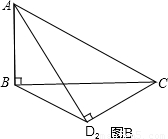
 把△ABC、△ADC沿对角线AC翻折交AD、BC于点F、E.
把△ABC、△ADC沿对角线AC翻折交AD、BC于点F、E. ,将矩形沿对角线AC剪开,解答以下问题:
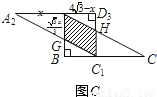
,将矩形沿对角线AC剪开,解答以下问题: ),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.
),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.



 ,将矩形沿对角线AC剪开,解答以下问题:
,将矩形沿对角线AC剪开,解答以下问题: ),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.
),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.



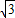 ,将矩形沿对角线AC剪开,解答以下问题:
,将矩形沿对角线AC剪开,解答以下问题: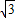 ),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.
),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.