Question

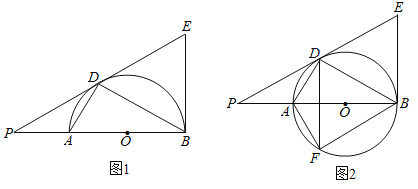
【题目】如图1，在△ABC中，∠ABC=90°，AO是△ABC的角平分线，以O为圆心，OB为半径作圆交BC于点D，

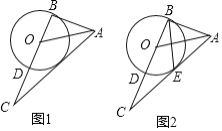
（1）求证：直线AC是⊙O的切线；

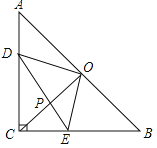
（2）在图2中，设AC与⊙O相切于点E，连结BE，如果AB=4，tan∠CBE=．

①求BE的长；②求EC的长．

Answer 1

【答案】(1)见解析;(2)①；②.

【解析】

(1)作作OE⊥AC,由AO是∠BAC的角平分线,得到∠BAO＝∠EAO,判断出△ABO≌△AEO（AAS）,得到OE＝OB,所以直线AC是⊙O的切线;

(2)先利用AE与⊙O相切于点E， AB＝AE＝4,再用三角函数求出OB,BC,然后用三角形相似,得到BC＝2CE， ,用勾股定理求出CD,最后用切割线定理即可

证明：（1）如图1，

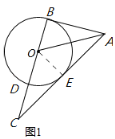
作OE⊥AC， ∴∠OEA＝90°，

∵∠ABC＝90，∴∠OEA＝∠ABC，

∵AO是△ABC的角平分线，∴∠BAO＝∠EAO，

在△ABO和△AEO中， ，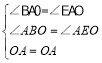

∴△ABO≌△AEO（AAS），∴OE＝OB，

∵OB是⊙O的半径，∴OE是⊙O的半径， ∴直线AC是⊙O的切线；

（2）①如图2，∵∠ABO＝90°，

∴AB切⊙O于B，

∵AE与⊙O相切于点E， ∴AB＝AE＝4，

∵AO是△ABC的角平分线， ∴AO⊥BE， ∴∠BAO+∠ABE＝90°，

∵∠CBE+∠ABE＝90°， ∴∠BAO＝∠CBE，

∵tan∠CBE＝ ， ∴tan∠BAO＝ ，

在Rt△ABO中，AB＝4，tan∠BAO＝ ， ∴ ， ∴BD＝2OB＝4，

∵AB是⊙O的直径， ∴∠BED＝90°，

又∵tan∠CBE＝ ＝ ， ∴BE＝2DE，

在Rt△BDE中， ∵BE2+DE2＝BD2， ∴ ， 解得 ；

②∵AC是⊙O的切线， ∴∠CED＝∠CBE，

∵∠DCE＝∠ECB，∴△CDE∽△CEB， ∴ ，

又∵tan∠CBE＝ ＝ ， ∴BC＝2CE， ，

∵BD＝BC﹣CD ∴ ， 解得 ．