Question

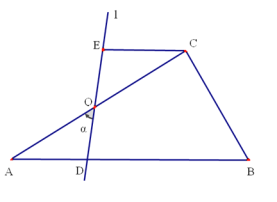
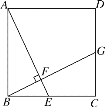
【题目】已知，矩形ABCD中，AB＝6cm，BC＝18cm，AC的垂直平分线EF分别交AD、BC于点E、F，垂足为O．

（1）如图1，连接AF、CE．求证四边形AFCE为菱形，并求AF的长；

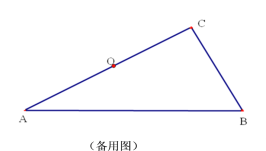
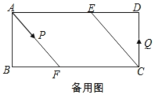
（2）如图2，动点P、Q分别从A、C两点同时出发，沿△AFB和△CDE各边匀速运动一周．即点P自A→F→B→A停止，点Q自C→D→E→C停止．在运动过程中．

①已知点P的速度为每秒10cm，点Q的速度为每秒6cm，运动时间为t秒，当A、C、P、Q四点为顶点的四边形是平行四边形时，求t的值．

②若点P、Q的运动路程分别为x、y（单位：cm，xy≠0），已知A、C、P、Q四点为顶点的四边形是平行四边形，求x与y满足的函数关系式．

Answer 1

【答案】（1）证明见解析，；（2）①，②．

【解析】

（1）首先证明，由此得出，从而证明四边形为菱形，然后在Rt△ABF中利用勾股定理进一步求解即可；

（2）①根据题意依次发现当点在上时，点在上以及点在上时，点在或上，也不能构成平行四边形，当点在上、点在上时，才能构成平行四边形，据此进一步求解即可；②以、、、四点为顶点的四边形是平行四边形时，根据题意分当点在上、点在上时或当点在上、点在上时以及当点在上、点在上时三种情况进一步分析求解即可.

（1）证明：∵四边形是矩形，

∴，

∴，．

∵垂直平分，垂足为，

∴，

在和△COF中，

∵

∴，

∴，

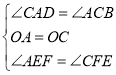
∴四边形为平行四边形，

又∵，

∴四边形为菱形，

设菱形的边长，则

在Rt△ABF中，，

解得：，

∴；

（2）①显然当点在上时，点在上，此时、、、四点不可能构成平行四边形；

同理点在上时，点在或上，也不能构成平行四边形．因此只有当点在上、点在上时，才能构成平行四边形．

∴以、、、四点为顶点的四边形是平行四边形时，，

∵点的速度为每秒，点的速度为每秒，运动时间为秒，

∴，，

∴，

解得：，

∴以、、、四点为顶点的四边形是平行四边形时，；

②由题意得，以、、、四点为顶点的四边形是平行四边形时，点、在互相平行的对应边上．

分三种情况：

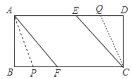
其一：如图1，当点在上、点在上时，，，即；

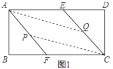
其二：如图2，当点在上、点在上时，，，即；

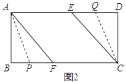
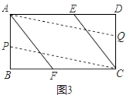
其三：如图3，当点在上、点在上时，，，即，

综上所述，与满足的函数关系式是．