Question

(本题10分)在平面直角坐标系中，如图1，将个边长为1的正方形并排组成矩形OABC,相邻两边OA和OC分别落在轴和轴的正半轴上, 设抛物
（＜0）过矩形顶点B、C.
（1）当n=1时，如果=-1，试求b的值；
（2）当n=2时，如图2，在矩形OABC上方作一边长为1的正方形EFMN，使EF在线段CB上，如果M，N两点也在抛物线上，求出此时抛物线的解析式；
（3）将矩形OABC绕点O顺时针旋转，使得点B落到轴的正半轴上，如果该抛物线同时经过原点O.①试求当n=3时a的值；
②直接写出关于的关系式．

Answer 1

(本题10分)
（1）由题意可知，抛物线对称轴为直线x=，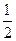
∴,得b= 1； ……2分
（2）设所求抛物线解析式为，
由对称性可知抛物线经过点B（2，1）和点M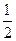（，2）
∴   解得    
∴所求抛物线解析式为；……4分
（3）①当n=3时，OC=1，BC=3，
设所求抛物线解析式为，
过C作CD⊥OB于点D，则Rt△OCD∽Rt△CBD，
∴,       
设OD=t，则CD=3t，
∵，  
∴， ∴,
∴C（，）,  又B（，0），                                               
∴把B 、C坐标代入抛物线解析式，得
  解得:a=；   ……2分
②.     ……2分

解析