题目内容
如图：在等腰△ABC中，∠C=90º，AC=6，D 是AC上一点，若tan∠DBA=,则A D的长为（ ） 
A． | B．2 | C．1 | D．2 |
B
解析考点：解直角三角形．
专题：计算题．
分析：作DE⊥AB，构造直角三角形，根据角的正弦值与三角形边的关系，可求出各边的长．解答：解：作DE⊥AB于E点．
∵tan∠DBA=
=
，
∴BE=5DE，
∵△ABC为等腰直角三角形，
∴∠A=45°，
∴AE=DE．
∴BE=5AE，
又∵AC=6，
∴AB=6 ．
∴AE+BE=5AE+AE=6 ，
∴AE= ，
∴在等腰直角△ADE中，由勾股定理，得AD= AE=2．
故选B．
点评：此题的关键是作辅助线，构造直角三角形，运用三角函数的定义建立关系式然后求解．
练习册系列答案
课堂小作业系列答案
黄冈小状元口算速算练习册系列答案
成功训练计划系列答案
倍速训练法直通中考考点系列答案
一卷搞定系列答案
名校作业本系列答案
相关题目
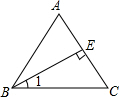如图，在等腰△ABC中，AB=AC，BE⊥AC，垂足为E，则∠1与∠A的关系式为（ ）| A、∠1=∠A | ||
B、∠1=
| ||
| C、∠1=2∠A | ||
| D、无法确定 |
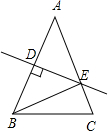如图，在等腰△ABC中，AB=AC，AB的垂直平分线DE交AB于点D，交另一腰AC于点E，若∠EBC=15°，则∠A=
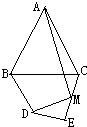24、如图，在等腰△ABC中，AB=AC，∠ABC=α，在四边形BDEC中，DB=DE，∠BDE=2α，M为CE的中点，连接AM，DM．
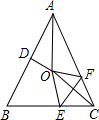（2012•丽水）如图，在等腰△ABC中，AB=AC，∠BAC=50°．∠BAC的平分线与AB的中垂线交于点O，点C沿EF折叠后与点O重合，则∠CEF的度数是
如图，在等腰△ABC中，AB=AC=10cm，直线DE垂直平分AB，分别交AB、AC于D、E两点．若BC=8cm，则△BCE的周长是