题目内容
在△ABC中，D是BC的中点，CE⊥AD于E，BF⊥AD于F，F在AD的延长线上．说明CE=BF的理由．
证明：如图，∵
在△ABC中，D是BC的中点，
∴CD=BD．
又∵CE⊥AD于E，BF⊥AD于F，
∴∠CED=∠BFD=90°，
∴在△CDE与△BDF中，
，
∴△CDE≌△BDF（AAS），
∴CE=BF．
分析：通过全等三角形的判定定理AAS证得△CDE≌△BDF，则全等三角形的对应边相等：CE=BF．
点评：本题考查了全等三角形的判定与性质．注意充分利用图中的隐含条件：对顶角相等．
在△ABC中，D是BC的中点，∴CD=BD．
又∵CE⊥AD于E，BF⊥AD于F，
∴∠CED=∠BFD=90°，
∴在△CDE与△BDF中，
，∴△CDE≌△BDF（AAS），
∴CE=BF．
分析：通过全等三角形的判定定理AAS证得△CDE≌△BDF，则全等三角形的对应边相等：CE=BF．
点评：本题考查了全等三角形的判定与性质．注意充分利用图中的隐含条件：对顶角相等．
练习册系列答案
相关题目
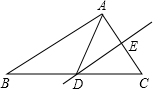如图所示，在△ABC中，DE是AC的中垂线，AE=3cm，△ABD得周长为13cm，则△ABC的周长是
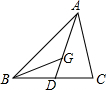如图，在△ABC中，AD是中线，G是重心，
如图在△ABC中，AD是BC边上的高，BE平分∠ABD，交AD于E．已知∠BED=60°，∠BAC=50°，则∠C=（ ）