题目内容
【题目】如图,⊙O与正方形ABCD的两边AB、AD相切,且DE与⊙O相切于E点.若正方形ABCD的周长为44,且DE=6,则sin∠ODE= . 
【答案】![]()
【解析】
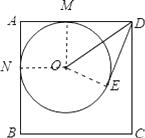
∵四边形ABCD是正方形,正方形ABCD的周长为44,
∴AD=AB=11,∠A=90°,
∵圆O与正方形ABCD的两边AB、AD相切,
∴∠OMA=∠ONA=90°=∠A,
∵OM=ON,
∴四边形ANOM是正方形,
∵AD和DE与圆O相切,
∴OE⊥DE,DM=DE=6,
∴AM=11﹣6=5,
∴OM=ON=OE=5,在RT△ODM中,OD= ![]() =
= ![]() =
= ![]() ,
,
∵OE=OM=5,
∴sin∠ODE= ![]() =
= ![]() .
.
故答案为: ![]() .
.
设切线AD的切点为M,切线AB的切点为N,连接OM、ON、OE,先证出正方形ANOM,求出AM长,根据勾股定理切点OD的长,根据解直角三角形求出即可.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目