题目内容
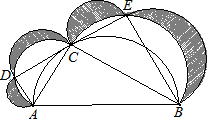 如图,以AB为直径作半圆与直角梯形ABED另一腰DE相切于C点,再分别以AC、BC、
如图,以AB为直径作半圆与直角梯形ABED另一腰DE相切于C点,再分别以AC、BC、AD、CD、CE、BE为直径作半圆.若AC=3,BC=4,则图中阴影部分的面积和为
分析:先取AB的中点O,连接OC,由勾股定理求出AB的长,再根据切线的性质判断出OC是梯形ABED的中位线,求出OC的长,根据直角梯形的性质及勾股定理求出CE的长,进而求出梯形的高,再根据勾股定理及圆的面积公式得出S阴影=S梯形ABED-S△ABC,再把相应的数值代入进行计算即可.
解答: 解:取AB的中点O,连接OC,
解:取AB的中点O,连接OC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵AC=3,BC=4,
∴AB=
=
=5,
∵DE是⊙O的切线,
∴OC⊥DE,
∵梯形ABED是直角梯形,
∴∠ADC=∠BEC=90°,
∴OC是梯形ABED的中位线,
∴CD=CE,
=OC,
∴OA=OC=
=
,
∵梯形ABED是直角梯形,
∴∠ADC=∠BEC=90°,
∴AC2-AD2=BC2-BE2,即32-(2OC-BE)2=42-BE2,即32-(5-BE)2=42-BE2,解得BE=3.2,
∴CD=CE=
=
=
,
∴DE=2CE=2×
=
,
∵△ACD是直角三角形,
∴AC2=AD2+CD2,
∴(
)2=(
)2+(
)2,
即以AC为半径的圆的半圆的面积等于以CD为半径的半圆与以AD为半径的半圆面积的和,
∴以CD为半径的半圆阴影部分与以AD为半径的半圆阴影部分面积的和等于Rt△ACD的面积,
同理可得,以BE为半径的半圆阴影部分与以CE为半径的半圆阴影部分面积的和等于Rt△CBE的面积,
∴S阴影=S梯形ABED-S△ABC=
-
AC×BC=OC×DE-
AC×BC=2.5×
-
×3×4=6.
故答案为:6.
 解:取AB的中点O,连接OC,
解:取AB的中点O,连接OC,∵AB是⊙O的直径,
∴∠ACB=90°,
∵AC=3,BC=4,
∴AB=
| AC2+BC2 |
| 32+42 |
∵DE是⊙O的切线,
∴OC⊥DE,
∵梯形ABED是直角梯形,
∴∠ADC=∠BEC=90°,
∴OC是梯形ABED的中位线,
∴CD=CE,
| AD+BE |
| 2 |
∴OA=OC=
| AB |
| 2 |
| 5 |
| 2 |
∵梯形ABED是直角梯形,
∴∠ADC=∠BEC=90°,
∴AC2-AD2=BC2-BE2,即32-(2OC-BE)2=42-BE2,即32-(5-BE)2=42-BE2,解得BE=3.2,
∴CD=CE=
| BC2-BE2 |
| 42-3.22 |
| 12 |
| 5 |
∴DE=2CE=2×
| 12 |
| 5 |
| 24 |
| 5 |
∵△ACD是直角三角形,
∴AC2=AD2+CD2,
∴(
| AC |
| 2 |
| CD |
| 2 |
| AD |
| 2 |
即以AC为半径的圆的半圆的面积等于以CD为半径的半圆与以AD为半径的半圆面积的和,
∴以CD为半径的半圆阴影部分与以AD为半径的半圆阴影部分面积的和等于Rt△ACD的面积,
同理可得,以BE为半径的半圆阴影部分与以CE为半径的半圆阴影部分面积的和等于Rt△CBE的面积,
∴S阴影=S梯形ABED-S△ABC=
| (AD+BE)×DE |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 24 |
| 5 |
| 1 |
| 2 |
故答案为:6.
点评:本题考查的是切线的性质、勾股定理及直角梯形的性质,解答此题的关键是作出辅助线,构造出梯形的中位线,再根据中位线的性质进行解答.

练习册系列答案
相关题目
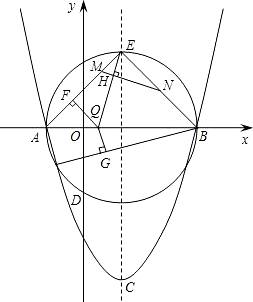 请说明理由.
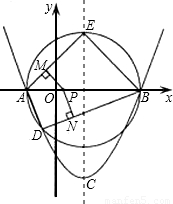
请说明理由.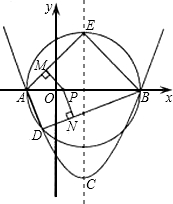 已知:抛物线y=ax2+bx+c(a≠0),顶点C(1,-3),与x轴交于A,B两点,A(-1,0).
已知:抛物线y=ax2+bx+c(a≠0),顶点C(1,-3),与x轴交于A,B两点,A(-1,0). 已知:抛物线y=ax2+bx+c(a≠0),顶点C(1,-3),与x轴交于A,B两点,A(-1,0).
已知:抛物线y=ax2+bx+c(a≠0),顶点C(1,-3),与x轴交于A,B两点,A(-1,0).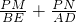 是否为定值?若是,请求出此定值;若不是,请说明理由;
是否为定值?若是,请求出此定值;若不是,请说明理由;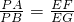 是否成立?若成立,请给出证明;若不成立,请说明理由.
是否成立?若成立,请给出证明;若不成立,请说明理由.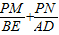 是否为定值?若是,请求出此定值;若不是,请说明理由;
是否为定值?若是,请求出此定值;若不是,请说明理由;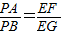 是否成立?若成立,请给出证明;若不成立,请说明理由.
是否成立?若成立,请给出证明;若不成立,请说明理由.