题目内容
如图,P是Rt△ABC的斜边BC上异于B、C的一点,过P点作直线截△ABC,使截得的三角形与△ABC相似,满足这样条件的直线共有( )
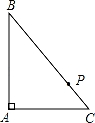
A.1条 B.2条 C.3条 D.4条
C【考点】相似三角形的判定.
【分析】过点P作直线与另一边相交,使所得的三角形与原三角形有一个公共角,只要再作一个直角就可以.
【解答】解:由于△ABC是直角三角形,
过P点作直线截△ABC,则截得的三角形与△ABC有一公共角,
所以只要再作一个直角即可使截得的三角形与Rt△ABC相似,
过点P可作AB的垂线、AC的垂线、BC的垂线,共3条直线.
故选:C.

【点评】本题主要考查三角形相似判定定理及其运用.解题时,运用了两角法(有两组角对应相等的两个三角形相似)来判定两个三角形相似.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目



 C.x(x﹣1)=182 D.x(x﹣1)=182×2
C.x(x﹣1)=182 D.x(x﹣1)=182×2
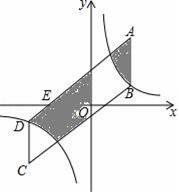

 x+1,当自变量x取m时,对应的函数值大于0,设自变量分别取m﹣3,m+3时对应的函数值为y1,y2,则下列判断正确的是( )
x+1,当自变量x取m时,对应的函数值大于0,设自变量分别取m﹣3,m+3时对应的函数值为y1,y2,则下列判断正确的是( )