��Ŀ����
����Ŀ���Ѵ���ʽͨ����յ��ֶΣ��õ��ֲ���ȫƽ��ʽ���ٽ����й�����ͽ��⣬���ֽ��ⷽ�������䷽����
�磺�����䷽���ֽ���ʽ��a2+6a+8��
�⣺ԭʽ=a2+6a+8+1-1=a2+6a+9-1
=(a+3)2��12=![]()
��M=a2-2a��1�������䷽����M����Сֵ��
�⣺![]()
��(a-b)2��0���൱a=1ʱ��M����Сֵ��2��
������������Ͻ���������⣺
��1�����䷽����ʽ�ֽ⣺![]() ��
��
��2����![]() ����M����Сֵ��
����M����Сֵ��
��3����֪x2+2y2+z2-2xy-2y-4z+5=0����x+y+z��ֵ��
���𰸡���1��![]() ����2��
����2��![]() ����3��4��
����3��4��
��������
��1�������䷽������ճ�һ����ȫƽ����ʽ�������ù�ʽ��������ʽ�ֽ⼴�ɣ�
��2���������䷽������ճ�һ����ȫƽ����ʽ���ٸ���ż�η��ķǸ�����⼴�ɣ�
��3���������䷽��������ʽ�ֽ⣬������ż�η��ķǸ������x��y��z��ֵ��Ȼ�������⼴�ɣ�
��1��ԭʽ![]()
![]()
![]()
![]()
![]() ��
��
��2��![]()
![]()
![]()
![]()
![]()
![]() ��
��![]() ʱ��
ʱ��![]() ����Сֵ
����Сֵ![]() ��
��
��3��![]()
![]()
![]()
![]()
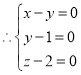
���![]()
��![]() ��
��

��ϰ��ϵ�д�
 ��������������������ϵ�д�
��������������������ϵ�д�
�����Ŀ