��Ŀ����
��ͼ����ֱ֪��y=-x+2�������ύ��A��B���㣬��P��x���ϣ���1����A��B��������ꣻ
��2��Բ��P�뾶r=
 ������P��ֱ��AB����ʱ����Բ��P�����ꣻ
������P��ֱ��AB����ʱ����Բ��P�����ꣻ��3������P��ֱ��AB����ʱ��ǡ��һ����������ΪC��2��2����������y=ax2+bx+c����Բ��P��������������x��������������ұߵĽ���ΪM����x���Ϸ�ͬʱҲ��ֱ��AB�Ϸ������������Ƿ����һ��Q��ʹ�ı���ABMQ�������������ڣ������������������������ڣ���˵�����ɣ�

���𰸡���������1��ֱ��AB�Ľ���ʽ�У���x=0������õ�A�����ꣻ��y=0������õ�B�����꣮
��2�����ڵ�P��λ�ò�ȷ������ô��Ҫ��������������ٵ�P��ֱ��AB��ࡢ�ڵ�P��ֱ��AB�Ҳࣻ����ķ���������ͬ����Բ����ֱ��AB�Ĵ��ߣ��ڹ�����ֱ���������У�����Բ�İ뾶��ֱ���������е�����ǣ�����ȷ��Բ��P�����꣮
��3���������ô���ϵ����ȷ�������ߵĽ���ʽ��������δ֪����ʾ��M�����ꣻ��ͼ��֪���ı���ABMQ����������ı���AOMQ�͡�ABO���������ã��ɴ˵õ������ı���ABMQ�������M�������ĺ�����ϵ���ɺ��������ʿ��ж��ı���ABMQ�Ƿ������������
��� �⣺��1����x=0ʱ��y=2����y=0ʱ��x=2��
�⣺��1����x=0ʱ��y=2����y=0ʱ��x=2��
����A��0��2����B��2��0����
��2������P���������˶�ʱ��P��ֱ��AB���������������
��һ���������ͼ������P��ֱ��AB�������ֱ��AB����ʱ�����е�D1��D1P1��x����P1��
��Rt��D1P1B�У���OBD1=45°��D1P1= ��
��
����BP1=2��ǡ��P1��O���غϣ�����Ϊ��0��0����
�ڶ����������ͼ������P��ֱ��AB���Ҳ���ֱ��AB����ʱ�����е�D2��D2P2��x����P2��
��Rt��D2P2B�У���P2BD2=45°��D2P2=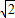 ��
��
����BP2=2��OP2=4����P���������4��0����
 ��3����ͼ��3��������y=ax2+bx+c��ԭ��O���Ҷ�������Ϊ��2��2����
��3����ͼ��3��������y=ax2+bx+c��ԭ��O���Ҷ�������Ϊ��2��2����
����y=a��x-2��2+2����x=0ʱy=0��
���a=- ������y=-
������y=- x2+2x��
x2+2x��
����x���Ϸ����������ϴ��ڵ�Qʹ�ı���ABMQ��������Q����Ϊ��m��- m2+2m��������OQ���������
m2+2m��������OQ���������
S�ı���ABMQ=S��AOQ+S��OMQ-S��AOB
= m×2+
m×2+ ×4×��-
×4×��- m2+2m��-
m2+2m��- ×2×2
×2×2
=-m2+5m-2=-��m- ��2+
��2+ ��
��
��m= ʱ��S�ı���ABMQ�����ֵΪ
ʱ��S�ı���ABMQ�����ֵΪ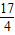 ��
��
�����飬��Q�� ��
��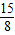 ����ֱ��AB�Ϸ������ԣ���x���Ϸ�ͬʱҲ��ֱ��AB�Ϸ����������ϴ��ڵ�Qʹ�ı���ABMQ��������S�ı���ABMQ�����ֵΪ
����ֱ��AB�Ϸ������ԣ���x���Ϸ�ͬʱҲ��ֱ��AB�Ϸ����������ϴ��ڵ�Qʹ�ı���ABMQ��������S�ı���ABMQ�����ֵΪ ��
��
���������⿼���˺�������ʽ��ȷ����Բ��ֱ�ߵ�λ�ù�ϵ��ͼ������Ľⷨ���ۺ�֪ʶ����2�����ڽ��ʱ��P�������λ�������ױ����ӵĵط���
��2�����ڵ�P��λ�ò�ȷ������ô��Ҫ��������������ٵ�P��ֱ��AB��ࡢ�ڵ�P��ֱ��AB�Ҳࣻ����ķ���������ͬ����Բ����ֱ��AB�Ĵ��ߣ��ڹ�����ֱ���������У�����Բ�İ뾶��ֱ���������е�����ǣ�����ȷ��Բ��P�����꣮
��3���������ô���ϵ����ȷ�������ߵĽ���ʽ��������δ֪����ʾ��M�����ꣻ��ͼ��֪���ı���ABMQ����������ı���AOMQ�͡�ABO���������ã��ɴ˵õ������ı���ABMQ�������M�������ĺ�����ϵ���ɺ��������ʿ��ж��ı���ABMQ�Ƿ������������
���
 �⣺��1����x=0ʱ��y=2����y=0ʱ��x=2��
�⣺��1����x=0ʱ��y=2����y=0ʱ��x=2������A��0��2����B��2��0����
��2������P���������˶�ʱ��P��ֱ��AB���������������
��һ���������ͼ������P��ֱ��AB�������ֱ��AB����ʱ�����е�D1��D1P1��x����P1��
��Rt��D1P1B�У���OBD1=45°��D1P1=
 ��
������BP1=2��ǡ��P1��O���غϣ�����Ϊ��0��0����
�ڶ����������ͼ������P��ֱ��AB���Ҳ���ֱ��AB����ʱ�����е�D2��D2P2��x����P2��
��Rt��D2P2B�У���P2BD2=45°��D2P2=
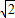 ��
������BP2=2��OP2=4����P���������4��0����
 ��3����ͼ��3��������y=ax2+bx+c��ԭ��O���Ҷ�������Ϊ��2��2����
��3����ͼ��3��������y=ax2+bx+c��ԭ��O���Ҷ�������Ϊ��2��2��������y=a��x-2��2+2����x=0ʱy=0��
���a=-
 ������y=-
������y=- x2+2x��
x2+2x������x���Ϸ����������ϴ��ڵ�Qʹ�ı���ABMQ��������Q����Ϊ��m��-
 m2+2m��������OQ���������
m2+2m��������OQ���������S�ı���ABMQ=S��AOQ+S��OMQ-S��AOB
=
 m×2+
m×2+ ×4×��-
×4×��- m2+2m��-
m2+2m��- ×2×2
×2×2=-m2+5m-2=-��m-
 ��2+
��2+ ��
����m=
 ʱ��S�ı���ABMQ�����ֵΪ
ʱ��S�ı���ABMQ�����ֵΪ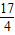 ��
�������飬��Q��
 ��
��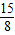 ����ֱ��AB�Ϸ������ԣ���x���Ϸ�ͬʱҲ��ֱ��AB�Ϸ����������ϴ��ڵ�Qʹ�ı���ABMQ��������S�ı���ABMQ�����ֵΪ
����ֱ��AB�Ϸ������ԣ���x���Ϸ�ͬʱҲ��ֱ��AB�Ϸ����������ϴ��ڵ�Qʹ�ı���ABMQ��������S�ı���ABMQ�����ֵΪ ��
�����������⿼���˺�������ʽ��ȷ����Բ��ֱ�ߵ�λ�ù�ϵ��ͼ������Ľⷨ���ۺ�֪ʶ����2�����ڽ��ʱ��P�������λ�������ױ����ӵĵط���

��ϰ��ϵ�д�
�����Ŀ
 16����ͼ����ֱ֪��AB��CD�ཻ�ڵ�O����COE��ֱ�ǣ�OFƽ�֡�AOE��
16����ͼ����ֱ֪��AB��CD�ཻ�ڵ�O����COE��ֱ�ǣ�OFƽ�֡�AOE�� 5����ͼ����ֱ֪��l1��l2��AB��CD����1=30�㣬���2�Ķ���Ϊ��������
5����ͼ����ֱ֪��l1��l2��AB��CD����1=30�㣬���2�Ķ���Ϊ�������� ��ͼ����ֱ֪��l1��
��ͼ����ֱ֪��l1�� ��2013•��������ͼ����ֱ֪��a��b����1=35�㣬���2=
��2013•��������ͼ����ֱ֪��a��b����1=35�㣬���2= ��ͼ����ֱ֪��m��n�������н��۳������ǣ�������
��ͼ����ֱ֪��m��n�������н��۳������ǣ�������