题目内容
【题目】已知![]() 的半径为5,弦AB的长度为m,点C是弦AB所对优弧上的一动点.
的半径为5,弦AB的长度为m,点C是弦AB所对优弧上的一动点.
![]() 如图
如图![]() ,若
,若![]() ,则
,则![]() 的度数为______
的度数为______![]() ;
;
![]() 如图
如图![]() ,若
,若![]() .
.
![]() 求
求![]() 的正切值;
的正切值;
![]() 若
若![]() 为等腰三角形,求
为等腰三角形,求![]() 面积.
面积.

【答案】![]() 30;
30;![]() 的正切值为
的正切值为![]() ;
;![]() 或
或![]() .
.
【解析】
![]() 连接OA,OB,判断出
连接OA,OB,判断出![]() 是等边三角形,即可得出结论;
是等边三角形,即可得出结论;
![]() 先求出
先求出![]() ,再用勾股定理求出
,再用勾股定理求出![]() ,进而求出
,进而求出![]() ,即可得出结论;
,即可得出结论;
![]() 分三种情况,利用等腰三角形的性质和垂径定理以及勾股定理即可得出结论.
分三种情况,利用等腰三角形的性质和垂径定理以及勾股定理即可得出结论.
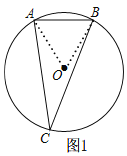
![]() 如图1,连接OB,OA,
如图1,连接OB,OA,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 是等边三角形,
是等边三角形,
![]() ,
,
![]() ,
,
故答案为30;
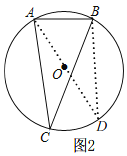
![]() 如图2,连接AO并延长交
如图2,连接AO并延长交![]() 于D,连接BD,
于D,连接BD,
![]() 为
为![]() 的直径,
的直径,
![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,根据勾股定理得,
,根据勾股定理得,![]() ,
,
![]() ,
,
![]() ,
,
![]() 的正切值为
的正切值为![]() ;
;
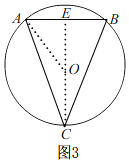
![]() Ⅰ、当
Ⅰ、当![]() 时,如图3,连接CO并延长交AB于E,
时,如图3,连接CO并延长交AB于E,
![]() ,
,![]() ,
,
![]() 为AB的垂直平分线,
为AB的垂直平分线,
![]() ,
,
在![]() 中,
中,![]() ,根据勾股定理得,
,根据勾股定理得,![]() ,
,
![]() ,
,
![]() ;
;
Ⅱ、当![]() 时,如图4,
时,如图4,
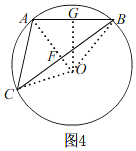
连接OA交BC于F,
![]() ,
,![]() ,
,
![]() 是BC的垂直平分线,
是BC的垂直平分线,
过点O作![]() 于G,
于G,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
Ⅲ、当![]() 时,如图5,由对称性知,
时,如图5,由对称性知,![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目