题目内容
已知Rt△ABC≌Rt△A′B′C′，∠C=∠C′=90°，AB=5，BC=4，AC=3，则△A′B′C′的周长为________，面积为________，斜边上的高为________．
12 6 
分析：此题先求出△ABC的周长和面积及斜边上的高，再运用全等三角形的性质即可求出，△A′B′C′的周长、面积、斜边上的高．
解答：Rt△ABC中，AB=5，BC=4，AC=3，
∴△ABC的周长是5+4+3=12，
△ABC的面积是
AC•BC=×3×4=6，
△ABC的斜边上的高是h，面积是：
，则h=，
∵Rt△ABC≌Rt△A′B′C′，
∴△A′B′C′的周长为12，面积为6，斜边上的高为．
故分别填12，6，．
点评：本题考查了全等三角形性质的应用，确认线段、角、周长，面积，对应边上的对应高相等，往往利用全等三角形的性质求解．
分析：此题先求出△ABC的周长和面积及斜边上的高，再运用全等三角形的性质即可求出，△A′B′C′的周长、面积、斜边上的高．
解答：Rt△ABC中，AB=5，BC=4，AC=3，
∴△ABC的周长是5+4+3=12，
△ABC的面积是
AC•BC=×3×4=6，△ABC的斜边上的高是h，面积是：
，则h=，∵Rt△ABC≌Rt△A′B′C′，
∴△A′B′C′的周长为12，面积为6，斜边上的高为
．故分别填12，6，
．点评：本题考查了全等三角形性质的应用，确认线段、角、周长，面积，对应边上的对应高相等，往往利用全等三角形的性质求解．
练习册系列答案
相关题目
已知Rt△ABC中，∠C=90°，AC=8cm，BC=6cm．则其内心和外心之间的距离是（ ）
| A、10cm | ||
| B、5cm | ||
C、
| ||
| D、2cm |
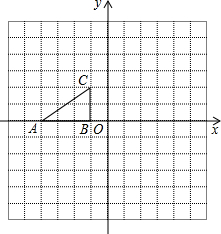如图，每个小方格都是边长为1个单位的正方形．Rt△ABC 的顶点在格 点上，建立平面直角坐标系后，点A的坐标为（-4，0），点B的坐标为（-1，0）．已知Rt△ABC和Rt△A1B1C1关于y轴对称，Rt△A1B1C1和Rt△A2B2C2关于直线y=-2轴对称．