题目内容
已知:AC是⊙O的直径,PA⊥AC,连结OP,弦CB//OP,直线PB交直线AC于点D,BD=2PA.【小题1】证明:直线PB是⊙O的切线;
【小题2】探索线段PO与线段BC之间的数量关系,并加以证明;
【小题3】求sin∠OPA的值.

【小题1】连结OB.∵BC//OP, ∴∠BCO=∠POA,∠CBO=∠POB.
又∵OC=OB,∴∠BCO=∠CBO, ∴∠POB=∠POA.
又∵PO=PO,OB=OA, ∴△POB≌△POA.
∴∠PBO=∠PAO=90°. ∴PB是⊙O的切线.
【小题1】2PO=3BC(写PO=
 BC亦可).
BC亦可).证明:∵△POB≌△POA,∴PB=PA.
∵BD=2PA,∴BD=2PB.
∵BC//OP,∴△DBC∽△DPO.
∴
 .∴2PO=3BC.
.∴2PO=3BC.注:开始没有写出判断结论,正确证明也给满分.

【小题1】∵△DBC∽△DPO,∴
 ,即DC=
,即DC= OD.∴DC=2OC.
OD.∴DC=2OC.设OA=x,PA=y.则OD=3x,DB=2y.
在Rt△OBD中,由勾股定理,得(3x)2= x2+(2y)2.即2 x2= y2.
∵x>0,y>0,∴y=
 x.OP=
x.OP= .
.∴sin∠OPA=
 .解析:
.解析:根据切线定理证明圆的切线,有关计算的依据是三角形相似和勾股定理。

练习册系列答案
相关题目
 如图,在平面直角坐标系中,直
如图,在平面直角坐标系中,直 (2013•南通一模)已知:如图,直y=2x+b交x轴于点B,交y轴于点C,点A为x轴正半轴上一点,AO=CO,△ABC的面积为12.
(2013•南通一模)已知:如图,直y=2x+b交x轴于点B,交y轴于点C,点A为x轴正半轴上一点,AO=CO,△ABC的面积为12. 如图,在平面直角坐标系中,直
如图,在平面直角坐标系中,直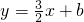 与双曲线
与双曲线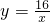 相交于第一象限内的点A,AB、AC分别垂直于x轴、y轴,垂足分别为B、C,已知四边形ABCD是正方形,求直线所对应的一次函数的解析式以及它与x轴的交点E的坐标.
相交于第一象限内的点A,AB、AC分别垂直于x轴、y轴,垂足分别为B、C,已知四边形ABCD是正方形,求直线所对应的一次函数的解析式以及它与x轴的交点E的坐标.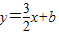 与双曲线
与双曲线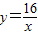 相交于第一象限内的点A,AB、AC分别垂直于x轴、y轴,垂足分别为B、C,已知四边形ABCD是正方形,求直线所对应的一次函数的解析式以及它与x轴的交点E的坐标.
相交于第一象限内的点A,AB、AC分别垂直于x轴、y轴,垂足分别为B、C,已知四边形ABCD是正方形,求直线所对应的一次函数的解析式以及它与x轴的交点E的坐标.