题目内容
抛物线y=x2+bx+1的图象与x轴只有一个公共点，则b等于
- A.2
- B.-2
- C.±2
- D.0
C
分析：令y=0，则关于x的一元二次方程x2+bx+1=0的根的判别式△=0，据此列出关于b的新方程，通过解新方程即可求得b的值．
解答：令y=0，则当抛物线y=x2+bx+1的图象与x轴只有一个公共点时，关于x的一元二次方程x2+bx+1=0的根的判别式△=0，即b2-4=0，
解得b=±2．
故选C．
点评：本题考查了抛物线与x轴的交点．解题时，运用“二次函数y=ax2+bx+c与x轴的交点个数与系数的关系：当b2-4ac=0时，只有一个交点”求解即可．
分析：令y=0，则关于x的一元二次方程x2+bx+1=0的根的判别式△=0，据此列出关于b的新方程，通过解新方程即可求得b的值．
解答：令y=0，则当抛物线y=x2+bx+1的图象与x轴只有一个公共点时，关于x的一元二次方程x2+bx+1=0的根的判别式△=0，即b2-4=0，
解得b=±2．
故选C．
点评：本题考查了抛物线与x轴的交点．解题时，运用“二次函数y=ax2+bx+c与x轴的交点个数与系数的关系：当b2-4ac=0时，只有一个交点”求解即可．
练习册系列答案
相关题目
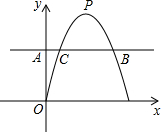且与直线AB交于另一点C（在B的左边），抛物线的顶点为P．
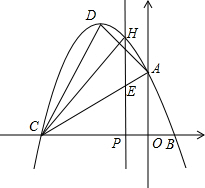已知：m，n是方程x2-6x+5=0的两个实数根，且m＜n，抛物线y=-x2+bx+c的图象经过点B（m，0），A（0，n）
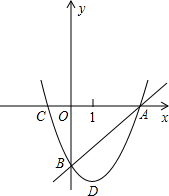（2013•普陀区二模）如图，抛物线y=x2+bx-c经过直线y=x-3与坐标轴的两个交点A、B，此抛物线与x轴的另一个交点为C，抛物线的顶点为D．