题目内容
24、(答案不全)
(1)在如图(1)所示的正方体表面展开图中的三个空白正方形内各填入一个质数,使该图复原成正方体后,三组对面上的两数之和都相等.
(2)图(2)是由四个如图(1)所示的正方体拼成的长方体,其中有阴影的面上为合数,无阴影的面上为质数,并且整个表面上任意两个相邻正方形内的数都不是图(1)所示的正方体相对面上的两数.已知长方体正面上的四个数之和为质数,那么其左侧面上的数是
(3)如果把图(2)中的长方体从中间等分成左右两个小长方体,它们各自表面上的各数之和分别为S左和S右,那么S左与S右的大小关系是S左
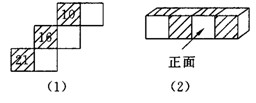
(1)在如图(1)所示的正方体表面展开图中的三个空白正方形内各填入一个质数,使该图复原成正方体后,三组对面上的两数之和都相等.
(2)图(2)是由四个如图(1)所示的正方体拼成的长方体,其中有阴影的面上为合数,无阴影的面上为质数,并且整个表面上任意两个相邻正方形内的数都不是图(1)所示的正方体相对面上的两数.已知长方体正面上的四个数之和为质数,那么其左侧面上的数是
21
(填具体数).(3)如果把图(2)中的长方体从中间等分成左右两个小长方体,它们各自表面上的各数之和分别为S左和S右,那么S左与S右的大小关系是S左
>
S右.
分析:(1)最小的质数是2,它应是21的对面,这两个数加起来的和是23,那么18的对面是质数5,10的对面是质数13,可得从上到下依次填7、2、13;
(2)已知长方体正面上的四个数之和为质数,任意两个相邻正方形内的数都不是图(1)所示的正方体相对面上的两数.那么可猜测正面上的四个数分别为:13,18,2,21,按照(1),13在正面,那么21应该在左侧.
(3)分开后,左侧表面的数的和为:(13+21+10+18)+(18+10+2+17)=109;右侧表面的数的和为:(2+18+10+21)+(21+18+13+2)=105∴S左>S右.
(2)已知长方体正面上的四个数之和为质数,任意两个相邻正方形内的数都不是图(1)所示的正方体相对面上的两数.那么可猜测正面上的四个数分别为:13,18,2,21,按照(1),13在正面,那么21应该在左侧.
(3)分开后,左侧表面的数的和为:(13+21+10+18)+(18+10+2+17)=109;右侧表面的数的和为:(2+18+10+21)+(21+18+13+2)=105∴S左>S右.
解答:解:(1)如图.

(2)21.

(2)21.
点评:正方体的空间图形,应从相对面入手,分析及解答问题.如没有空间观念,动手操作可很快得到答案.

练习册系列答案
相关题目
为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取整数,满分为100分)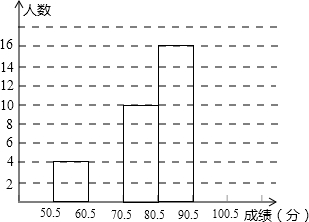 进行统计.请你根据尚未完成并有局部污损的频率分布和频率分布直方图,解答下列问题(将答案直接填在横线上):
进行统计.请你根据尚未完成并有局部污损的频率分布和频率分布直方图,解答下列问题(将答案直接填在横线上):
(1)填充频率分布表的空格;
(2)补全频数直方图;
(3)在该问题中,总体、个体、样本和样本容量各是什么?
(4)全体参赛学生中,竞赛成绩落在哪组范围内的人数最多?
(5)若成绩在90分以上(不含90分)为优秀,则该校成绩优秀的约为多少人?
 进行统计.请你根据尚未完成并有局部污损的频率分布和频率分布直方图,解答下列问题(将答案直接填在横线上):
进行统计.请你根据尚未完成并有局部污损的频率分布和频率分布直方图,解答下列问题(将答案直接填在横线上):| 分组 | 频数 | 频率 |
| 50.5~60.5 | 4 | 0.08 |
| 60.5~70.5 | 0.16 | |
| 70.5~80.5 | 10 | |
| 80.5~90.5 | 16 | 0.32 |
| 90.5~100.5 | ||
| 合计 | 50 | 1.00 |
(2)补全频数直方图;
(3)在该问题中,总体、个体、样本和样本容量各是什么?
(4)全体参赛学生中,竞赛成绩落在哪组范围内的人数最多?
(5)若成绩在90分以上(不含90分)为优秀,则该校成绩优秀的约为多少人?
 12、如图,点E在AB上,AC=AD,请你添加一个条件,使图中存在全等三角形,所添条件为
12、如图,点E在AB上,AC=AD,请你添加一个条件,使图中存在全等三角形,所添条件为 (2012•牡丹江)如图.点D、E在△ABC的边BC上,AB=AC,AD=AE.请写出图中的全等三角形
(2012•牡丹江)如图.点D、E在△ABC的边BC上,AB=AC,AD=AE.请写出图中的全等三角形