题目内容
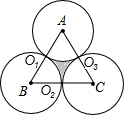 如图,正△ABC的边长为6,分别以A、B、C为圆心,3为半径的圆两两相切于O1、O2、O3,求
如图,正△ABC的边长为6,分别以A、B、C为圆心,3为半径的圆两两相切于O1、O2、O3,求 |
| O1O2 |
 |
| O2O3 |
 |
| O3O1 |
考点:相切两圆的性质,等边三角形的性质,扇形面积的计算
专题:
分析:观察发现,阴影部分的面积等于正三角形ABC的面积减去三个圆心角是60°,半径是3的扇形的面积.
解答: 解:连接AO2.
解:连接AO2.
∵△ABC是正三角形,BO2=CO2=3,
∴∠BAC=∠B=∠C=60°,AO2⊥BC.
∴AO2=3
.
∴阴影部分的面积=
×6×3
-3×
=9
-
π.
 解:连接AO2.
解:连接AO2.∵△ABC是正三角形,BO2=CO2=3,
∴∠BAC=∠B=∠C=60°,AO2⊥BC.
∴AO2=3
| 3 |
∴阴影部分的面积=
| 1 |
| 2 |
| 3 |
| 60π×32 |
| 360 |
| 3 |
| 9 |
| 2 |
点评:此题主要考查了相切两圆的性质以及扇形面积公式,能够正确计算正三角形的面积和扇形的面积是解题关键.

练习册系列答案
相关题目
下列变形正确的是( )
A、
| ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、
|
关于x的方程mx2+2x+1=0无实数根,则m的取值范围是( )
| A、m≠0 | B、m>1 |
| C、m<1且m≠0 | D、m>-1 |
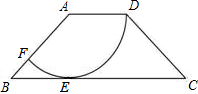 如图,在四边形ABCD中,AD∥BC,AD=2,AB=2
如图,在四边形ABCD中,AD∥BC,AD=2,AB=2