题目内容
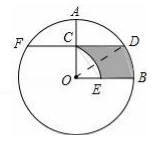
【题目】如图,在⊙O中,半径OA⊥OB,过点OA的中点C作FD∥OB交⊙O于D、F两点,且CD=![]() ,以O为圆心,OC为半径作
,以O为圆心,OC为半径作![]() ,交OB于E点.
,交OB于E点.
(1)求⊙O的半径OA的长;
(2)计算阴影部分的面积.

【答案】(1)2;(2)![]() .
.
【解析】
试题分析:(1)首先证明OA⊥DF,由OD=2CO推出∠CDO=30°,设OC=x,则OD=2x,利用勾股定理即可解决问题.(2)根据S圆=S△CDO+S扇形OBD﹣S扇形OCE计算即可.
试题解析:(1)连接OD,
∵OA⊥OB,
∴∠AOB=90°,
∵CD∥OB,
∴∠OCD=90°,
在RT△OCD中,∵C是AO中点,CD=![]() ,
,
∴OD=2CO,设OC=x,
∴x2+(![]() )2=(2x)2,
)2=(2x)2,
∴x=1,
∴OD=2,
∴⊙O的半径为2.
(2)∵sin∠CDO=![]() =
=![]() ,
,
∴∠CDO=30°,
∵FD∥OB,
∴∠DOB=∠ODC=30°,
∴S圆=S△CDO+S扇形OBD﹣S扇形OCE
=![]() ×
×![]() +
+![]() ﹣
﹣![]()
=![]() +
+![]() .
.

练习册系列答案
相关题目


