题目内容
已知抛物线 与x轴有两个不同的交点.
与x轴有两个不同的交点.
(1)求c的取值范围;
(2)抛物线 与x轴两交点的距离为2,求c的值.
与x轴两交点的距离为2,求c的值.
解:(1)∵抛物线 与x轴有两个不同的交点,
与x轴有两个不同的交点,
得出b2-4ac>0,
∴1-4× c>0,
c>0,
解得:c<
(2)设抛物线 与x轴的两交点的横坐标为x1,x2,
与x轴的两交点的横坐标为x1,x2,
∵两交点间的距离为2,∴x1-x2=2,由题意,得x1+x2=-2
解得x1=0,x2=-2,
∴ =x1•x2=0,
=x1•x2=0,
即c的值为0.
分析:(1)根据抛物线 与x轴有两个不同的交点,得出b2-4ac>0,进而求出k的取值范围.
与x轴有两个不同的交点,得出b2-4ac>0,进而求出k的取值范围.
(2)根据两交点间的距离为2,∴x1-x2=2,由题意,得x1+x2=-2,求出即可.
点评:此题主要考查了二次函数y=ax2+bx+c的图象与x轴交点的个数的判断以及图象与坐标轴交点的性质,熟练掌握其性质是解题关键.
 与x轴有两个不同的交点,
与x轴有两个不同的交点,得出b2-4ac>0,
∴1-4×
 c>0,
c>0,解得:c<

(2)设抛物线
 与x轴的两交点的横坐标为x1,x2,
与x轴的两交点的横坐标为x1,x2,∵两交点间的距离为2,∴x1-x2=2,由题意,得x1+x2=-2
解得x1=0,x2=-2,
∴
 =x1•x2=0,
=x1•x2=0,即c的值为0.
分析:(1)根据抛物线
 与x轴有两个不同的交点,得出b2-4ac>0,进而求出k的取值范围.
与x轴有两个不同的交点,得出b2-4ac>0,进而求出k的取值范围.(2)根据两交点间的距离为2,∴x1-x2=2,由题意,得x1+x2=-2,求出即可.
点评:此题主要考查了二次函数y=ax2+bx+c的图象与x轴交点的个数的判断以及图象与坐标轴交点的性质,熟练掌握其性质是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
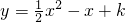 与x轴有两个交点.
与x轴有两个交点.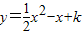 与x轴有两个交点.
与x轴有两个交点. 与x轴有两个交点,则m的取值范围是
与x轴有两个交点,则m的取值范围是
 与x轴有两个交点,则m的取值范围是
与x轴有两个交点,则m的取值范围是  与x轴有两个交点,则m的取值范围是
.
与x轴有两个交点,则m的取值范围是
.