��Ŀ����
����Ŀ�������ϵ�A��Ӧ����Ϊa����B��Ӧ����Ϊb����A�ڸ����ᣬ��|a|=6��b����С����ż����
��1�����߶�AB�ij���
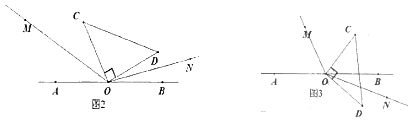
��2������C�������϶�Ӧ����Ϊx����x�Ƿ���2x+1=3x��9�Ľ⣬���������Ƿ���ڵ�P��ʹ��PA��PB��![]() BC��AB�������ڣ������P��Ӧ�������������ڣ�˵�����ɣ�
BC��AB�������ڣ������P��Ӧ�������������ڣ�˵�����ɣ�
��3����ͼ����Q��B���Ҳ�һ�㣬QA���е�ΪM��NΪQB���ĵȷֵ��ҿ�����Q�㣬��Q��B���Ҳ��˶�ʱ��˵����QM��![]() BN��ֵ���䣬�������ֵ��
BN��ֵ���䣬�������ֵ��
![]()
���𰸡���1��8����2�����ڣ���P��Ӧ����Ϊ-8��4����3��4
��������
��1���ȸ����������a��b��ֵ������AB�ij���
��2���Ƚⷽ�����x��ֵ���ó���C�������϶�Ӧ�������Ӷ��ó�PA+PB=12�����P�Ķ�Ӧ��Ϊm���ٷ�3��������۷������ֱ���ʽ���㼴�ɣ�
��3�����Q�Ķ�Ӧ��Ϊt���ú�t��ʽ�ӱ�ʾ��QM��BN����֤�����ۣ�
�⣺��1��������ã�a=-6��b=2��
��AB=2-(-6)=8��
��2����2x+1=3x��9
��ã�x=10
���C��Ӧ����Ϊ10��
��BC=10-2=8��AB=2-(-6)=8��
��![]() BC��AB=12=PA��PB
BC��AB=12=PA��PB
���P�Ķ�Ӧ��Ϊm��
�ٵ�P��A���ʱ��-6-m+2-m=12����ã�m=-8��
�ڵ�P��A�Ҳ�ʱ��6+m+m-2=12����ã�m=4��
�۵�P��AB֮��ʱ��PA+PB=8��ȥ��
���P�Ķ�Ӧ��Ϊ-8��4��
��3�����Q�Ķ�Ӧ��Ϊt��
��QA=t-(-6)=t+6��QB=t-2
��MΪQA���е�
��![]()
��NΪQB���ĵȷֵ�
��![]()
��![]()
��QM��![]() BN��ֵ���䣬��ֵΪ4��
BN��ֵ���䣬��ֵΪ4��

 �Ǽ�����������ϵ�д�
�Ǽ�����������ϵ�д� â���̸������Ծ�ϵ�д�
â���̸������Ծ�ϵ�д�