Question

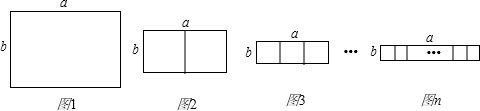
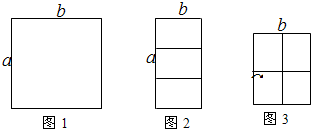
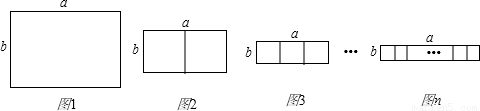
将现有一根长为1的铁丝．
（1）若把它截成四段然后围成图1所示的“口”形的矩形框，当矩形框的长a与矩形框的宽b满足a=    b时所围成的矩形框面积最大．
（2）若把它截成六段，①可以围成图2所示的“目”形的矩形框，当矩形框的长a与矩形框的宽b满足a=    b时所围成的矩形框面积最大； ②可以围成图3所示的“田”形矩形框，当矩形框的长a与矩形框的宽b满足a=    b时所围成的矩形框面积最大．

Answer 1

【答案】分析：（1）根据长度为1，可得出a与b的关系式，然后可表示出图1的面积，利用配方法求最值即可；
（2）根据长度为1，可得出a与b的关系式，然后可表示出图2、图3的面积，利用配方法求最值即可；
解答：解：（1）由题意得，2a+2b=1，则b=，
此时S=ab=a×=-a²+a=-（a-）²+，
当a=时，面积S最大，则a=，b=，
即a=b时，面积最大；
（2）①由题意得，2a+4b=1，则b=，
此时S=ab=a×=-a²+a=-（a-）²+，
当a=时，面积S最大，则a=，b=，
即a=2b时，面积最大；
②由题意得，3a+3b=1，则b=，
此时S=ab=a×=-a²+a=-（a-）²+，
当a=时，面积S最大，则a=，b=，
即a=b时，面积最大．
故答案为：1；2、1．
点评：本题考查了二次函数的应用，解答本题的关键是根据铁丝长度为1得出a与b的关系式，注意掌握配方法求函数的最值，难度一般．