题目内容
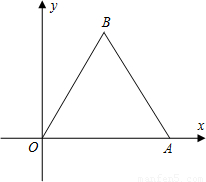
边长为4的等边三角形的面积为分析:根据等边三角形三线合一的性质可以求得高线AD的长度,根据BC和AD即可求得三角形的面积.
解答: 解:∵等边三角形三线合一,
解:∵等边三角形三线合一,
∴D为BC的中点,BD=DC=2,
在Rt△ABD中,AB=4,BD=2,
∴AD=
=2
,
∴等边△ABC的面积为
BC•AD=
×4×2
=4
.
故答案为 4
.
 解:∵等边三角形三线合一,
解:∵等边三角形三线合一,∴D为BC的中点,BD=DC=2,
在Rt△ABD中,AB=4,BD=2,
∴AD=
| AB2-BD2 |
| 3 |
∴等边△ABC的面积为
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
故答案为 4
| 3 |
点评:本题考查了勾股定理在直角三角形中的运用,考查了三角形面积的计算,考查了等边三角形各边长相等的性质,本题中根据勾股定理即可AD的长度是解题的关键.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目

 重合,连接AD并延长交BC的延长结于P.
重合,连接AD并延长交BC的延长结于P. 27、阅读:我们把边长为1的等边三角形PQR沿着边长为整数的正n(n>3)边形的边按照如图1的方式连续转动,当顶点P回到正n边形的内部时,我们把这种状态称为它的“点回归”;当△PQR回到原来的位置时,我们把这种状态称为它的“三角形回归”.
27、阅读:我们把边长为1的等边三角形PQR沿着边长为整数的正n(n>3)边形的边按照如图1的方式连续转动,当顶点P回到正n边形的内部时,我们把这种状态称为它的“点回归”;当△PQR回到原来的位置时,我们把这种状态称为它的“三角形回归”.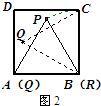


 (x>0)上.
(x>0)上. (x>0)的解析式;
(x>0)的解析式;