题目内容
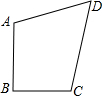 已知:如图,四边形ABCD,AB=1,BC=
已知:如图,四边形ABCD,AB=1,BC= ,CD=
,CD= ,AD=3,且AB⊥BC.则四边形ABCD的面积为________.
,AD=3,且AB⊥BC.则四边形ABCD的面积为________.

分析:连接AC,由已知条件结合勾股定理求得S△ABC、S△ACD的面积,从而求得四边形ABCD的面积.
解答:
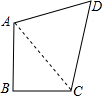 解:连接AC,
解:连接AC,∵AB⊥BC
∴△ABC是直角三角形
∴AC2=AB2+BC2=12+(
 )2=(
)2=( )2
)2∴AC=

∴S△ABC=
 AB•BC=
AB•BC= ×1×
×1× =
=
∵在△ACD中AC2+AD2=(
 )2+32=(
)2+32=( )2=CD2
)2=CD2∴△ACD是直角三角形.
∴S△ACD=
 AC•AD=
AC•AD= ×
× ×3=
×3=
∴四边形ABCD的面积为S△ABC+S△ACD=
 +
+ =
= .
.则四边形ABCD的面积为
 .
.点评:解答此题要用到勾股定理的逆定理:已知三角形ABC的三边满足a2+b2=c2,则三角形ABC是直角三角形.隐含了整体的数学思想和正确运算的能力.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
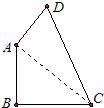 已知,如图,四边形ABCD中∠B=90°,AB=9,BC=12,AD=8,CD=17.
已知,如图,四边形ABCD中∠B=90°,AB=9,BC=12,AD=8,CD=17.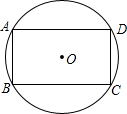 已知:如图,四边形ABCD内接于⊙O,且AB∥CD,AD∥BC,
已知:如图,四边形ABCD内接于⊙O,且AB∥CD,AD∥BC, 已知,如图,四边形ABCD是正方形,E、F分别是AB和AD延长线上的点,且BE=DF
已知,如图,四边形ABCD是正方形,E、F分别是AB和AD延长线上的点,且BE=DF 已知:如图,四边形ABCD中,BC=CD=10,AB=15,AB⊥BC,CD⊥BC,若把四边形ABCD绕直线AB旋转一周,则所得几何体的表面积是多少?
已知:如图,四边形ABCD中,BC=CD=10,AB=15,AB⊥BC,CD⊥BC,若把四边形ABCD绕直线AB旋转一周,则所得几何体的表面积是多少? 已知:如图,四边形ABCD及一点P.
已知:如图,四边形ABCD及一点P.