题目内容
如图,已知线段AB的长度是a(a>0),点C是线段AB上的一点,线段AC的长是线段AB与CB的长的比例中项,则线段AC的长为
分析:根据题意,设AC=x,则BC=a-x.根据比例中项的概念,得AB:AC=AC:CB,再根据比例的基本性质,可求得线段的长.
解答:解:设AC=x,则BC=a-x,
∵AB:AC=AC:CB,
∴a:x=x:a-x,
∴x2=a(a-x),即x2+ax-a2=0,
解得,x=
a.
∴线段AC的长为
a.
∵AB:AC=AC:CB,
∴a:x=x:a-x,
∴x2=a(a-x),即x2+ax-a2=0,
解得,x=
| ||
| 2 |
∴线段AC的长为
| ||
| 2 |
点评:理解比例中项的概念,能够根据比例的基本性质把比例式转换为等积式,解方程的时候注意a是字母已知数.

练习册系列答案
相关题目

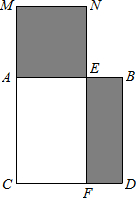 如图,已知线段AB的长为1,以AB为边在AB下方作正方形ACDB.取AB边上一点E,以AE为边在AB的上方作正方形AENM.过E作EF⊥CD,垂足为F点.若正方形AENM与四边形EFDB的面积相等,设AE=x,可列方程为
如图,已知线段AB的长为1,以AB为边在AB下方作正方形ACDB.取AB边上一点E,以AE为边在AB的上方作正方形AENM.过E作EF⊥CD,垂足为F点.若正方形AENM与四边形EFDB的面积相等,设AE=x,可列方程为 如图,已知线段AB的长为2.8cm.
如图,已知线段AB的长为2.8cm. 如图,已知线段AB的长度是acm,线段BC的长度比线段AB长度的2倍多5cm,线段AD的长度比线段BC长度的2倍少5cm.
如图,已知线段AB的长度是acm,线段BC的长度比线段AB长度的2倍多5cm,线段AD的长度比线段BC长度的2倍少5cm.