题目内容
 两条对角线的长为8cm和12cm的菱形纸片,两张重叠,下面的纸片不动,只将上面的纸片绕中心转90度,则会形成如图的图形,那么两图形没有重叠的部分的面积为________cm2.
两条对角线的长为8cm和12cm的菱形纸片,两张重叠,下面的纸片不动,只将上面的纸片绕中心转90度,则会形成如图的图形,那么两图形没有重叠的部分的面积为________cm2.
19.2
分析:首先利用菱形的性质和勾股定理,求得菱形的边长;再利用相似三角形判定与性质和三角形面积的计算方法解答即可.
解答: 解:如图,
解:如图,
∵四边形ABCD和四边形EFGH为相同的菱形,
∴OF=OA=6cm,OB=OE=4cm,且OA⊥OF,
∴BF=OF-OB=2cm,EF=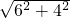 =2
=2 cm,
cm,
过M点作MN⊥OF,垂足为点N,
∴MN∥OA,
∴△BMN∽△BAO,△FMN∽△FEO,
∴ =
=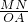 ,
, =
= ,设FM为x,则BM=2
,设FM为x,则BM=2 -x,
-x,
∴ =
= ,
,
即 =
= ,
,
解得x=
 cm,
cm,
从而MN=2.4cm,
所以两图形没有重叠的部分的面积为: ×BF×MN×8=
×BF×MN×8= ×2×2.4×8=19.2cm2.
×2×2.4×8=19.2cm2.
故填19.2.
点评:此题考查菱形的性质、勾股定理、相似三角形判定与性质和三角形面积的计算方法,是一道综合性较强的题目.
分析:首先利用菱形的性质和勾股定理,求得菱形的边长;再利用相似三角形判定与性质和三角形面积的计算方法解答即可.
解答:
 解:如图,
解:如图,∵四边形ABCD和四边形EFGH为相同的菱形,
∴OF=OA=6cm,OB=OE=4cm,且OA⊥OF,
∴BF=OF-OB=2cm,EF=
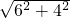 =2
=2 cm,
cm,过M点作MN⊥OF,垂足为点N,
∴MN∥OA,
∴△BMN∽△BAO,△FMN∽△FEO,
∴
 =
=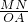 ,
, =
= ,设FM为x,则BM=2
,设FM为x,则BM=2 -x,
-x,∴
 =
= ,
,即
 =
= ,
,解得x=

 cm,
cm,从而MN=2.4cm,
所以两图形没有重叠的部分的面积为:
 ×BF×MN×8=
×BF×MN×8= ×2×2.4×8=19.2cm2.
×2×2.4×8=19.2cm2.故填19.2.
点评:此题考查菱形的性质、勾股定理、相似三角形判定与性质和三角形面积的计算方法,是一道综合性较强的题目.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
若一个菱形的边长为2,则这个菱形两条对角线的平方和为( )
| A、16 | B、8 | C、4 | D、1 |