题目内容
21、已知：如图所示，正方形ABCD的对角线相交于点O，点E、F分别在BC、DC边上
且∠EOF=90°，求证：△OEC≌△OFD．
且∠EOF=90°，求证：△OEC≌△OFD．
分析：分别求证∠1=∠3、OD=OC、∠OCE=∠ODF，进而根据ASA的方法即可求证△OEC≌△OFD．
解答：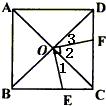
证明：在△OEC和△OFD中，
∵∠1+∠2=90°，∠2+∠3=90°，
∴∠1=∠3
AC、BD为正方形ABCD的对角线，
所以OD=OC，
∵正方形ABCD
∴∠OCE=∠ODF=45°
得△OEC≌△OFD．（ASA）
证明：在△OEC和△OFD中，∵∠1+∠2=90°，∠2+∠3=90°，
∴∠1=∠3
AC、BD为正方形ABCD的对角线，
所以OD=OC，
∵正方形ABCD
∴∠OCE=∠ODF=45°
得△OEC≌△OFD．（ASA）
点评：本题考查了正方形对角线互相垂直平分的性质，考查了正方形对角线即角平分线的性质，本题中正确的求证∠1=∠3是解题的关键．
练习册系列答案
相关题目
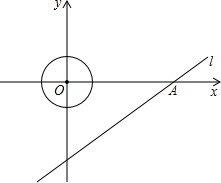
.5个单位/秒的速度运动，问在整个运动的过程中，点P在动圆的园面（圆上和圆的内部）上一共运动了多长时间？
已知：如图所示，直线l的解析式为
，并且与x轴、y轴分别交于点A、B.
x-3，并且与x轴、y轴分别相交于点A、B．
x-3，并且与x轴、y轴分别相交于点A、B．