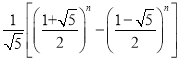Question

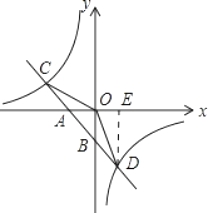
【题目】如图，已知一次函数y1=k1x+b的图象与x轴、y轴分别交于A、B两点，与反比例函数y2=的图象分别交于C、D两点，点D（2，﹣3），点B是线段AD的中点．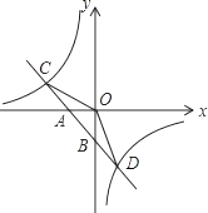

（1）求一次函数y1=k1x+b与反比例函数y2=的解析式；
（2）求△COD的面积；
（3）直接写出 k1x+b≥0 时自变量x的取值范围．
（4）动点P（0，m）在y轴上运动，当 |PCPD| 的值最大时，求点P的坐标．

Answer 1

【答案】
（1）解：∵点D（2，-3）在反比例函数y2=的图象上，
∴k2=2×（-3）=-6，
∴y2=.
作DE⊥x轴于E，
∵D（2，-3），点B是AD的中点，
∴A（-2，0），
∵A（-2，0），D（2，-3）在y1=k1x+b的图象上，
∴，
∴
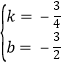
∴y1=-x.

（2）解：依题可得：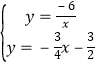
，
∴C（-4， ），
∴S△COD=S△AOC+S△AOD
=·AO ·yC+·AO·|yD|
=×2×（+3）
=.

（3）解：当x＜-4或0＜x＜2时，y1＞y2．

（4）解：C（-4，）关于y轴的对称点C′（4，）,延长C′D交y轴于点P，
∵D（2，-3），
设直线C′D解析式为：y=cx+d，
∴,
∴，
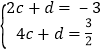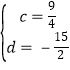∴直线C′D为 y=x ，
∴点P的坐标 为：（0， ）.

【解析】（1）将D（2，-3）代入反比例函数y2=，即可求出k2的值，从而球场反比例函数解析式；作DE⊥x轴于E，由D（2，-3），点B是AD中点得出A（-2，0），将A（-2，0），D（2，-3）坐标代入y1=k1xb，得到一个二元一次方程组，解之即可得出一次函数解析式.
（2）将反比例函数和一次函数解析式联立即可得出C（-4， ），再由S△COD=S△AOC+S△AOD=·AO ·yC+·AO·|yD|，代入数值即可得出答案.
（3）由图可得：当x＜-4或0＜x＜2时，y1＞y2．
（4）C（-4，）关于y轴的对称点C′（4，）,延长C′D交y轴于点，设直线C′D解析式为：y=cx+d，将C′和D点坐标代入得到一个二元一次方程组，解之即可得出直线C′D解析式，再令x=0即可求出点P的坐标.
【考点精析】解答此题的关键在于理解确定一次函数的表达式的相关知识，掌握确定一个一次函数，需要确定一次函数定义式y=kx+b（k不等于0）中的常数k和b．解这类问题的一般方法是待定系数法，以及对三角形的面积的理解，了解三角形的面积=1/2×底×高．