题目内容
关于x的方程 有两个不相等的实数根.
有两个不相等的实数根.
(1)求k的取值范围;
(2)是否存在实数k,使方程两个实数根的倒数和等于0?若存在,求出k的值,若不存在,说明理由.
解:(1)∵x的方程 有两个不相等的实数根.
有两个不相等的实数根.
∴△=(k+1)2-4k× >0,
>0,
∴2k+1>0,
∴k>- ,且k≠0;
,且k≠0;
(2)∵当方程两个实数根的倒数和等于0,
∴ =0,
=0,
∴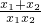 =0,
=0,
∴x1+x2=0,
∵x1+x2=-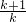 =0,
=0,
∴k=-1,
∵k>- ,
,
∴不存在实数k,使方程两个实数根的倒数和等于0.
分析:(1)根据x的方程 有两个不相等的实数根,得出△=(k+1)2-4k×
有两个不相等的实数根,得出△=(k+1)2-4k× >0,即可得出答案;
>0,即可得出答案;
(2)当方程两个实数根的倒数和等于0,得出 =0,进而得出k的值从而得出答案.
=0,进而得出k的值从而得出答案.
点评:此题主要考查了根的判别式和根与系数的关系,在解不等式时一定要注意数值的正负与不等号的变化关系,以及注意二次项系数不能为0.
 有两个不相等的实数根.
有两个不相等的实数根.∴△=(k+1)2-4k×
 >0,
>0,∴2k+1>0,
∴k>-
 ,且k≠0;
,且k≠0;(2)∵当方程两个实数根的倒数和等于0,
∴
 =0,
=0,∴
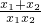 =0,
=0,∴x1+x2=0,
∵x1+x2=-
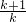 =0,
=0,∴k=-1,
∵k>-
 ,
,∴不存在实数k,使方程两个实数根的倒数和等于0.
分析:(1)根据x的方程
 有两个不相等的实数根,得出△=(k+1)2-4k×
有两个不相等的实数根,得出△=(k+1)2-4k× >0,即可得出答案;
>0,即可得出答案;(2)当方程两个实数根的倒数和等于0,得出
 =0,进而得出k的值从而得出答案.
=0,进而得出k的值从而得出答案.点评:此题主要考查了根的判别式和根与系数的关系,在解不等式时一定要注意数值的正负与不等号的变化关系,以及注意二次项系数不能为0.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
 有两个不相等的实数根x1,x2,求k的取值范围.
有两个不相等的实数根x1,x2,求k的取值范围.

 >0
>0
 有两个不相等实数根的概率.
有两个不相等实数根的概率. 有两个不相等的实数根x1,x2,求k的取值范围.
有两个不相等的实数根x1,x2,求k的取值范围.

 >0
>0
 有两个不相等的实数根,
有两个不相等的实数根, 有两个不相等的实数根.
有两个不相等的实数根.