Question

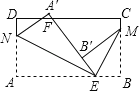
【题目】如图，四边形ABCD为矩形，将矩形ABCD沿MN折叠，折痕为MN，点B的对应点B′落在AD边上，已知AB＝6，AD＝4．

(1)若点B′与点D重合，连结DM，BN，求证：四边形BMB′N为菱形；

(2)在(1)问条件下求出折痕MN的长．

Answer 1

【答案】(1)证明见解析；(2)MN=.

【解析】

（1）首先证明四边形BMDN是平行四边形，再证明BM＝DM，即可证明四边形BMB'N为菱形.（2）首先设BM＝x，利用在Rt△AMB′中，结合勾股定理，求解x的值，在计算NQ，在Rt△MNQ中，利用勾股定理，即可得MN的长.

解：(1)由折叠可得，BM＝DM，∠BMN＝∠DMN，

∵CD∥AB，

∴∠BMN＝∠DNM，

∴∠DMN＝∠DNM，

∴DN＝DM，

∴BM＝MD＝DN，

又∵DN∥BM，

∴四边形BMDN是平行四边形，

又∵BM＝DM，

∴四边形BMB'N为菱形；

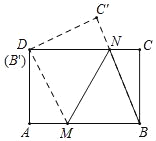
(2)设BM＝x，则DM＝x，AM＝6﹣x，

在Rt△AMB′中，由勾股定理可得，(6﹣x)2+42＝x2，

求解得x＝，

则DM＝＝DN，

如图，过点M作MQ⊥CD于点Q，则

NQ＝-(6-)＝，

在Rt△MNQ中，利用勾股定理可得MN＝ ＝．