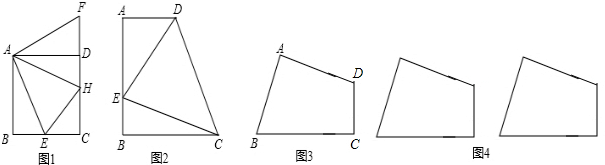
题目内容

如图①，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF=BE．

    (1)①试说明CE=CF，BCE=DCF；

    ②如图①，若点G在AD上，且GCE=450，则GE=GF成立吗?为什么?

    (2)运用(1)中积累的经验和知识，完成下题：

    如图②，在梯形ABCG中，AG∥BC，BC>AG，B=900，AB=BC=6，E是AB上 一点，且GCE=450，BE=2，求GE的长．   

(1)提示：①说明△BCE≌△DCF ②GE=G成立，说明△ECG≌△FCG即可． 

(2)过点C作CDAG，交AG的延长线于D，则得正方形ABCD．延长AD到点F，使DF=BE，连接CF．设GE=x，由(1)得GF=GE=x，则DG=x2，所以AG=6 (x2)=8x．在Rt△EAG中，42+(8x)2=x2，解得x=5，所以GE=5

练习册系列答案
相关题目
25、把正方形OFGE纸板按如图①方式放置在正方形纸板ABCD上，顶点G在对角线AC，并把正方形OFGE绕顶点A沿逆时针方向旋转，旋转角为а．
（1）如图②，当а=90°时，请直接写出线段DE与BF的数量关系和位置关系；
（2）如图③，当0°＜а＜90°时，（1）中的结论是否发生改变？若不变，请给出证明．若发生改变，请举例说明；
（3）如图④，将图①、图③中的两个正方形都改为矩形，其他条件不变，设AB=kAD（k＞0），当0°＜а＜90°时，（1）中的结论是否发生改变？若不变，请给出证明．若发生改变，请写出改变后的新结论，并给出证明．
（1）填空：如图1，在正方形PQRS中，已知点M、N分别在边QR、RS上，且QM=RN，连接PN、SM相交于点O，则∠POM=
 
度；
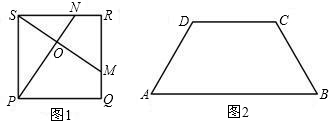（2）如图2，在等腰梯形ABCD中，已知AB∥CD，BC=CD，∠ABC=60度．以此为部分条件，精英家教网构造一个与上述命题类似的正确命题并加以证明．
26、如图1，在正方形ABCD中，若点E是△DBC内的一点，且DE=DC，BE=CE．
（1）连接AE．说明△ABE≌△DCE的理由；
（2）求∠BDE与∠CDE度数的比值；
（3）拓展探索：若只将题中的条件“正方形ABCD”换成条件“梯形ABCD中，AD∥BC，AB=DC，2∠DBC=∠DCB”．如图2，研究∠BDE与∠CDE度数的比值是否与（2）中的结论相同，写出你的研究结果并说明理由．
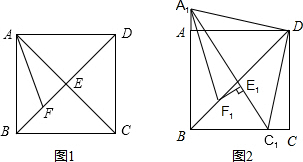精英家教网如图1，在正方形ABCD中，对角线AC与BD相交于点E，AF平分∠BAC，交BD于点F．
（1）求证：EF+
1
2
AC=AB；
（2）点C1从点C出发，沿着线段CB向点B运动（不与点B重合），同时点A1从点A出发，沿着BA的延长线运动，点C1与A1的运动速度相同，当动点C1停止运动时，另一动点A1也随之停止运动．如图2，A1F1平分∠BA1C1，交BD于点F1，过点F1作F1E1⊥A1C1，垂足为E1，请猜想E1F1，
1
2
A1C1与AB三者之间的数量关系，并证明你的猜想；
（3）在（2）的条件下，当A1E1=3，C1E1=2时，求BD的长．
课本练习拓展：
（1）如图1，在正方形ABCD中，E是BC上的一点，△ABE经过旋转后得到△ADF，
①旋转中心是点
A
A
；旋转角度最少是
90
90
度．
②爱动脑筋的小兵，在CD边上取点H使得∠HAE=45°，他发现：HE=BE+HD，他的发现正确吗？请你判断并说明理由．
（2）思维闯关：
如图2，在直角梯形ABCD中AD∥BC（BC＞AD），∠B=90°BC=AB=6，E是 AB上一点，且∠DCE=45°，BE=2，则DE的长=
5
5
．（小兵运用解答（1）中所积累的经验和知识做出了该题）
（3）动手闯过：
①小明有一块如图3所示的纸片，其中∠A=∠C=90°，AB=AD．小明请小兵只剪一刀后把它拼成正方形，请你帮助小兵在图中画出剪拼得示意图．
②小兵好朋友小红现有两块同小明一样的纸片，如图4，小兵能否在每块上各剪一刀，然后拼成一个大的正方形？若能，请你画出剪法和拼法的示意图；若不能，简要说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网