题目内容
设b≠c,且满足 ,则
,则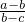 的值
的值
- A.大于零
- B.等于零
- C.小于零
- D.正负号不确定
C
分析:把a-b,b-c,看做一个整体,再利用恒等式a-c=a-b+b-c,进行运算可得问题的解.
解答:由题意得a-c=a-b+b-c,
∴( +1)(a-b)+
+1)(a-b)+ (b-c)=a-b+b-c,
(b-c)=a-b+b-c,
∴ (a-b)+(
(a-b)+( -1)(b-c)=0,
-1)(b-c)=0,
∴ (a-b)=(1-
(a-b)=(1- )(b-c),
)(b-c),
∵b≠c,
∴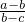 =
= .
.
∵1- <0,
<0,
∴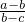 =
= <0.
<0.
故选C.
点评:本题考查和二次根式有关的运算和化简,在运算中注意整体思想的运用.
分析:把a-b,b-c,看做一个整体,再利用恒等式a-c=a-b+b-c,进行运算可得问题的解.
解答:由题意得a-c=a-b+b-c,
∴(
 +1)(a-b)+
+1)(a-b)+ (b-c)=a-b+b-c,
(b-c)=a-b+b-c,∴
 (a-b)+(
(a-b)+( -1)(b-c)=0,
-1)(b-c)=0,∴
 (a-b)=(1-
(a-b)=(1- )(b-c),
)(b-c),∵b≠c,
∴
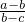 =
= .
.∵1-
 <0,
<0,∴
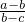 =
= <0.
<0.故选C.
点评:本题考查和二次根式有关的运算和化简,在运算中注意整体思想的运用.

练习册系列答案
相关题目
 ,则
,则 的值为
的值为 ,则以长为a,b,c的三条线段________构成三角形,(填“能”或“否”)
,则以长为a,b,c的三条线段________构成三角形,(填“能”或“否”) ,则m的值为 .
,则m的值为 . ,则x= .
,则x= .