题目内容
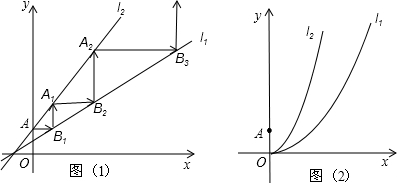
如图，（1）若点O为⊙O的圆心，则线段OA或OB或OC
OA或OB或OC
是圆O的半径；线段AB或BC或AC
AB或BC或AC
是圆O的弦，其中最长的弦是直径AC
直径AC
； |
| AB |
|
| BC |
|
| AB |
|
| BC |
|
| AC |
|
| AC |
（2）若∠A=40°，则∠ABO=
40°
40°
，∠C=50°
50°
，∠ABC=90°
90°
．分析：（1）根据半径、弦、直径及劣弧、半圆的定义作答；
（2）根据等边对等角可知∠ABO=∠A；先根据三角形内角和定理求出∠AOB，再由圆周角定理得出∠C=
∠AOB；根据直径所对的圆周角是直角可求出∠ABC的度数．
（2）根据等边对等角可知∠ABO=∠A；先根据三角形内角和定理求出∠AOB，再由圆周角定理得出∠C=
| 1 |
| 2 |
解答：解：（1）若点O为⊙O的圆心，则线段OA或OB或OC是圆O的半径；线段AB或BC或AC是圆O的弦，其中最长的弦是直径AC；
或
是劣弧；
是半圆．
（2）∵OA=OB，∠A=40°，
∴∠ABO=∠A=40°，
∵∠AOB+∠ABO+∠A=180°，
∴∠AOB=100°，
∠C═
∠AOB=50°，
∵AC是⊙O的直径，
∴∠ABC=90°．
故答案为：OA或OB或OC；AB或BC或AC，直径AC；
或
；
；
40°，50°，90°．
|
| AB |
|
| BC |
|
| AC |
（2）∵OA=OB，∠A=40°，
∴∠ABO=∠A=40°，
∵∠AOB+∠ABO+∠A=180°，
∴∠AOB=100°，
∠C═
| 1 |
| 2 |
∵AC是⊙O的直径，
∴∠ABC=90°．
故答案为：OA或OB或OC；AB或BC或AC，直径AC；
|
| AB |
|
| BC |
|
| AC |
40°，50°，90°．
点评：本题主要考查了圆的有关定义，三角形内角和定理，圆周角定理等知识．连接圆上任意两点的线段叫弦，经过圆心的弦叫直径，圆上任意两点间的部分叫圆弧，简称弧，圆的任意一条直径的两个端点把圆分成两条弧，每条弧都叫做半圆，大于半圆的弧叫做优弧，小于半圆的弧叫做劣弧．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
目标测试系列答案
相关题目
如图，（1）若点O为⊙O的圆心，则线段______是圆O的半径；线段______是圆O的弦，其中最长的弦是______；______是劣弧；______是半圆．
，图形l2为直线y=x+1，求点P从A到点A2的希望之旅程d2，并直接写出d3=______，d2010=______；
（x＞0），图形l2为抛物线y=x2（x＞0），求点P从A到点A2的希望之旅程d2，并直接写出dn=______．
