题目内容
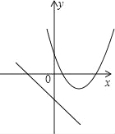
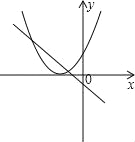
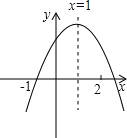
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出下列五条结论: ①abc<0;②4ac-b2<0;③4a+c<2b;④3b+2c<0;⑤m(am+b)+b<a(m≠-1).其中正确的结论是_________(把所有正确的结论的序号都填写在横线上)

【答案】②,④,⑤
【解析】
根据抛物线开口方向、对称轴、与y轴交点可判断①;根据抛物线与x轴交点个数可判断②;根据x=0与x=-2关于对称轴x=-1对称,且x=0时y>0,可判断③;根据x=1时,y<0,且对称轴为x=-1可判断④;由抛物线在x=-1时有最大值,可判断⑤.
①由抛物线图象得:开口向下,即a<0;c>0,-![]() =-1<0,即b=2a<0,
=-1<0,即b=2a<0,
∴abc>0,选项①错误;
②∵抛物线图象与x轴有两个交点,
∴△=b2-4ac>0,即4ac-b2<0,选项②正确;
③∵抛物线对称轴为x=-1,且x=0时,y>0,
∴当x=-2时,y=4a-2b+c>0,即4a+c>2b,选项③错误;
④∵抛物线对称轴x=-1,即-![]() =-1,
=-1,
∴a=![]() b,
b,
由图象可知,当x=1时,y=a+b+c=![]() +c<0,
+c<0,
故3b+2c<0,选项④正确;
⑤由图象可知,当x=-1时y取得最大值,
∵m≠-1,
∴am2+bm+c<a-b+c,即am2+bm+b<a,
∴m(am+b)+b<a,选项⑤正确;
故答案是:②④⑤.

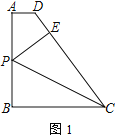
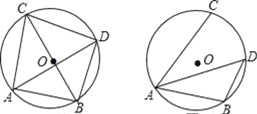
【题目】已知⊙O的直径为10,点A,点B,点C在⊙O上,∠CAB的平分线交⊙O于点D.
(Ⅰ)如图①,若BC为⊙O的直径,AB=6,求AC,BD,CD的长;
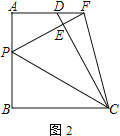
(Ⅱ)如图②,若∠CAB=60°,求BD的长.
【题目】某青年旅社有60间客房供游客居住,在旅游旺季,当客房的定价为每天200元时,所有客房都可以住满.客房定价每提高10元,就会有1个客房空闲,对有游客入住的客房,旅社还需要对每个房间支出20元/每天的维护费用,设每间客房的定价提高了x元.
(1)填表(不需化简)
入住的房间数量 | 房间价格 | 总维护费用 | |
提价前 | 60 | 200 | 60×20 |
提价后 |
|
|
|
(2)若该青年旅社希望每天纯收入为14000元且能吸引更多的游客,则每间客房的定价应为多少元?(纯收入=总收入﹣维护费用)