题目内容
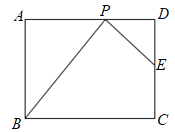
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是边
是边![]() 上一点,联结
上一点,联结![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于
于![]() 点,将
点,将![]() 沿直线
沿直线![]() 翻折,点
翻折,点![]() 落在点
落在点![]() ,若
,若![]() 为等腰三角形,则
为等腰三角形,则![]() 的长为__________.
的长为__________.
【答案】![]() 或1
或1
【解析】
若![]() 为等腰三角形,则需分以下三种情况进行讨论,①若
为等腰三角形,则需分以下三种情况进行讨论,①若![]() ,根据BP=PD列出方程即可解出;②若
,根据BP=PD列出方程即可解出;②若![]() ,作出辅助线,证明△ABP≌△
,作出辅助线,证明△ABP≌△![]() (AAS),根据等腰三角形的性质得出PF=DF=
(AAS),根据等腰三角形的性质得出PF=DF=![]() ,再结合全等三角形的性质得到AP=PF,列出方程求解即可;③若
,再结合全等三角形的性质得到AP=PF,列出方程求解即可;③若![]() ,作出辅助线,在Rt△
,作出辅助线,在Rt△![]() 中运用勾股定理列出方程求解即可.
中运用勾股定理列出方程求解即可.
解:设AP=x,则PD=3-x,
∵PE⊥BP,
∴![]() 沿直线
沿直线![]() 翻折后,PE⊥
翻折后,PE⊥![]()
∵四边形ABCD是矩形,
∴∠A=90°,
∴![]() ,
,
①若![]()
即BP=PD
∴![]()
解得:![]()
②若![]() ,
,
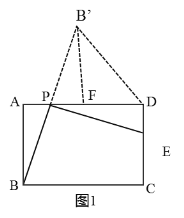
过点![]() 作
作![]() F⊥AD交AD于点F,如下图1所示,
F⊥AD交AD于点F,如下图1所示,
则PF=DF=![]()
又∵![]() ,∠A=∠
,∠A=∠![]() FP,∠APB=∠
FP,∠APB=∠![]() PF,
PF,
∴△ABP≌△![]() (AAS)
(AAS)
∴AP=PF
即![]()
解得:![]()
③若![]()
过点![]() 作
作![]() F⊥AD交AD于点F,如图1所示,
F⊥AD交AD于点F,如图1所示,
∵![]() ,∠A=∠
,∠A=∠![]() FP,∠APB=∠
FP,∠APB=∠![]() PF,
PF,
∴△ABP≌△![]() (AAS)
(AAS)
∴PF=AP=x,![]()
∴FD=3-2x,![]()
在Rt△![]() 中,
中,![]() ,
,
即![]() ,此方程无解,故不存在
,此方程无解,故不存在![]() 这种情况,
这种情况,
综上所述:![]() 的长为
的长为![]() 或1
或1

练习册系列答案
相关题目