题目内容
已知:四边形ABED中,AD⊥DE、BE⊥DE.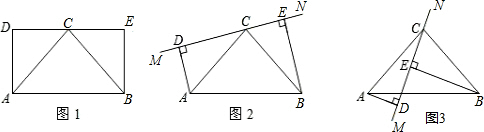
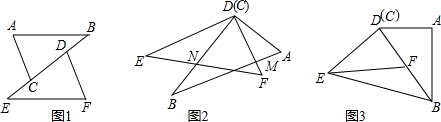
(1)如图1,点C是边DE的中点,且AB=2AD=2BE.判断△ABC的形状:______(不必说明理由);
(2)保持图1中△ABC固定不变,将直线DE绕点C旋转到图2中所在的MN的位置(垂线段AD、BE在直线MN的同侧).试探究线段AD、BE、DE长度之间有什么关系?并给予证明;
(3)保持图2中△ABC固定不变,继续绕点C旋转DE所在的直线MN到图3中的位置(垂线段AD、BE在直线MN的异侧).(2)中结论是否依然成立,若成立请证明;若不成立,请写出新的结论,并给予证明.
解:(1)等腰直角三角形.
理由:作CF⊥AB于点F.
∵AD⊥DE、BE⊥DE,
∴∠D=∠E=90°.
∵点C是边DE的中点,
∴CD=CE.
∵AB=2AD=2BE,
∴AD=BE= AB.
AB.
在△CDA和△CEB中
 ,
,
∴△CDA≌△CEB(SAS),
∴AC=BC,∠1=∠2.
∵CF⊥AB,
∴∠AFC=∠BFC=90°,AF=BF= AB.
AB.
.∴AF=AD=BF=BE.
在Rt△ADC和Rt△AFC中,
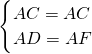 ,
,
∴Rt△ADC≌Rt△AFC(HL),
∴∠ACD=∠ACF.
在Rt△BEC和Rt△BFC中
 ,
,
∴Rt△BEC≌Rt△BFC(HL),
∴∠BCF=∠BCE.
∵∠ACD+∠ACF+∠BCF+∠BCE=180°
∴∠ACD=∠ACF=∠BCF=∠BCE=45°,
∴∠ACB=90°
∴△ACB是等腰直角三角形.
故答案为:等腰直角三角形;
(2)DE=AD+BE;
证明:如图2,
∵∠ACB=∠D=90°,
∵∠1+∠CAD=90°,∠1+∠2=90°,
∴∠CAD=∠2.
在Rt△ADC和Rt△CEB中,
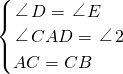 ,
,
∴△ADC≌△CEB(AAS),
∴DC=BE,CE=AD,
∵DE=DC+CE,
∴DE=BE+AD;
(3)DE=BE-AD
如图3,∵∠ACB=∠D=90°,
∵∠1+∠CAD=90°,∠1+∠2=90°,
∴∠CAD=∠2.
在Rt△ADC和Rt△CEB中,
 ,
,
∴△ADC≌△CEB(AAS),
∴DC=BE,CE=AD.
∵DE=DC-CE,
∴DE=BE-AD.
分析:(1)如图1,作CF⊥AB于点F.根据条件可以直接得出△CDA≌△CEB就可以得出AC=BC,∠ACB=90°而得出结论;
(2)如图2,由(1)的结论可以得出△ADC≌△CEB,就可以得出AD=CE,DC=EB进而可以得出结论;
(3)如图3,由(1)的结论可以得出△ADC≌△CEB,就可以得出AD=CE,DC=EB进而可以得出结论;,
点评:本题考查了等腰直角三角形的判定及性质的运用,全等三角形的判定及性质的运用,直角三角形的性质的运用,解答时证明三角形全等是关键.
理由:作CF⊥AB于点F.
∵AD⊥DE、BE⊥DE,
∴∠D=∠E=90°.
∵点C是边DE的中点,
∴CD=CE.
∵AB=2AD=2BE,
∴AD=BE=
 AB.
AB.在△CDA和△CEB中
 ,
,∴△CDA≌△CEB(SAS),
∴AC=BC,∠1=∠2.
∵CF⊥AB,
∴∠AFC=∠BFC=90°,AF=BF=
 AB.
AB..∴AF=AD=BF=BE.
在Rt△ADC和Rt△AFC中,
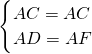 ,
,∴Rt△ADC≌Rt△AFC(HL),
∴∠ACD=∠ACF.
在Rt△BEC和Rt△BFC中
 ,
,∴Rt△BEC≌Rt△BFC(HL),
∴∠BCF=∠BCE.
∵∠ACD+∠ACF+∠BCF+∠BCE=180°
∴∠ACD=∠ACF=∠BCF=∠BCE=45°,
∴∠ACB=90°
∴△ACB是等腰直角三角形.
故答案为:等腰直角三角形;
(2)DE=AD+BE;
证明:如图2,
∵∠ACB=∠D=90°,

∵∠1+∠CAD=90°,∠1+∠2=90°,
∴∠CAD=∠2.
在Rt△ADC和Rt△CEB中,
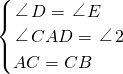 ,
,∴△ADC≌△CEB(AAS),
∴DC=BE,CE=AD,
∵DE=DC+CE,
∴DE=BE+AD;
(3)DE=BE-AD
如图3,∵∠ACB=∠D=90°,
∵∠1+∠CAD=90°,∠1+∠2=90°,
∴∠CAD=∠2.
在Rt△ADC和Rt△CEB中,
 ,
,∴△ADC≌△CEB(AAS),
∴DC=BE,CE=AD.
∵DE=DC-CE,
∴DE=BE-AD.
分析:(1)如图1,作CF⊥AB于点F.根据条件可以直接得出△CDA≌△CEB就可以得出AC=BC,∠ACB=90°而得出结论;
(2)如图2,由(1)的结论可以得出△ADC≌△CEB,就可以得出AD=CE,DC=EB进而可以得出结论;
(3)如图3,由(1)的结论可以得出△ADC≌△CEB,就可以得出AD=CE,DC=EB进而可以得出结论;,
点评:本题考查了等腰直角三角形的判定及性质的运用,全等三角形的判定及性质的运用,直角三角形的性质的运用,解答时证明三角形全等是关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
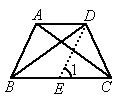
 23、已知:如图,梯形ABCD中,AD∥BC,E是BC的中点,∠BEA=∠DEA,连接AE、BD相交于点F,BD⊥CD.
23、已知:如图,梯形ABCD中,AD∥BC,E是BC的中点,∠BEA=∠DEA,连接AE、BD相交于点F,BD⊥CD.