Question

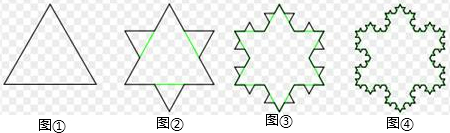
如图，把一个正三角形的每一边三等分，取中间一段为边向外作正三角形，并把这“中间一段”擦掉，重复上述两步，画出更小的正三角形；一直重复，直到无穷，所画出的曲线叫做“科镂曲线”，又称为“雪花曲线”．已知图①中正三角形的周长为C₁=3，图②中图形的周长C₂=4，按此规律下去，第5个图形的周长C₅=________．

Answer 1

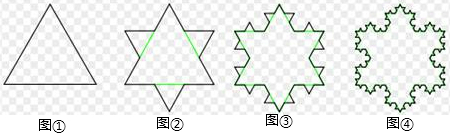
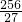
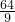分析：由于图①中正三角形的周长为C₁=3，观察图形得到图②在图①的基础上每边多了边长的，则图②中的图形的周长C₂=3+×3=3+1=4，图③在图②的基础上每边多了边长的，得到图③中正三角形的周长为C₃=4+××3×4=，于是得到图④中图形的周长C₄=+×××3×4×4，图⑤中图形的周长C₅=+××××3×4×4×4．
解答：图①中正三角形的周长为C₁=3，
图②中图形的周长C₂=3+×3=3+1=4，
图③中正三角形的周长为C₃=4+××3×4=，
图④中图形的周长C₄=+×××3×4×4=，
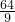图⑤中图形的周长C₅=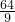+××××3×4×4×4=．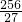
故答案为．
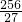点评：本题考查了规律型：图形的变化类：通过从一些特殊的图形变化中发现不变的因素或按规律变化的因素，然后推广到一般情况．