题目内容
 某单位计划在一块梯形空地种植草坪,并作出规划如图所示,其中AD=5米,BC=15米,AD∥BC,△ADE的面积是10平方米.已知每平方米草坪的造价为50元,单位共筹资金10000元,请通过计算说明所筹资金是否能将这块梯形空地植满草坪.
某单位计划在一块梯形空地种植草坪,并作出规划如图所示,其中AD=5米,BC=15米,AD∥BC,△ADE的面积是10平方米.已知每平方米草坪的造价为50元,单位共筹资金10000元,请通过计算说明所筹资金是否能将这块梯形空地植满草坪.分析:先求出△ADE和△CBE相似,再根据相似三角形对应边成比例列式求出两个三角形的相似比,再根据相似三角形面积的比等于相似比的平方求出△BCE的面积,再根据等高的三角形的面积的比等于底边的比求出△ABE和△CDE的面积,然后相加即可得解.
解答:解:∵四边形ABCD是梯形,AD∥BC,
∴∠ADE=∠CBE,
又∵∠AED=∠CEB(对顶角相等),
∴△ADE∽△CBE,
∴
=
=
=
=
,
∴
=(
)2=
,
∵S△ADE=10,
∴S△BCE=10×9=90,
∵
=
=
,
=
=
,
∴S△ABE=S△CDE=10×3=30,
∴S梯形ABCD=10+90+30+30=160,
∵160×50=8000<10000,
∴所筹资金能将这块梯形空地植满草坪.
∴∠ADE=∠CBE,
又∵∠AED=∠CEB(对顶角相等),
∴△ADE∽△CBE,
∴
| AD |
| BC |
| DE |
| BE |
| AE |
| EC |
| 5 |
| 15 |
| 1 |
| 3 |
∴
| S△ADE |
| S△BCE |
| AD |
| BC |
| 1 |
| 9 |
∵S△ADE=10,
∴S△BCE=10×9=90,
∵
| S△ADE |
| S△ABE |
| DE |
| BE |
| 1 |
| 3 |
| S△ADE |
| S△DEC |
| AE |
| EC |
| 1 |
| 3 |
∴S△ABE=S△CDE=10×3=30,
∴S梯形ABCD=10+90+30+30=160,
∵160×50=8000<10000,
∴所筹资金能将这块梯形空地植满草坪.
点评:本题考查了相似三角形的应用,主要利用了相似三角形的判定与对应边成比例的性质,等高的三角形的面积的比等于底边的比的性质.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
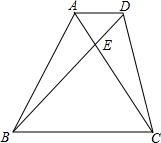 某单位计划在一块梯形空地种植草坪,并作出规划如图所示,其中AD=5米,BC=15米,AD∥BC,△ADE的面积是10平方米.已知每平方米草坪的造价为50元,单位共筹资金10000元,请通过计算说明所筹资金是否能将这块梯形空地植满草坪.
某单位计划在一块梯形空地种植草坪,并作出规划如图所示,其中AD=5米,BC=15米,AD∥BC,△ADE的面积是10平方米.已知每平方米草坪的造价为50元,单位共筹资金10000元,请通过计算说明所筹资金是否能将这块梯形空地植满草坪.