题目内容
已知二次函数y=-
| ||
| 3 |
| 3 |
(1)求点B坐标;
(2)点P从点C出发以每秒1个单位的速度沿线段CO向O点运动,到达点O后停止运动,过点P作PQ∥AC交OA于点Q,将四边形PQAC沿PQ翻折,得到四边形PQA′C′,设点P的运动时间为t.
①当t为何值时,点A′恰好落在二次函数y=-
| ||
| 3 |
②设四边形PQA′C′落在第一象限内的图形面积为S,求S关于t的函数关系式,并求出S的最大值.
分析:(1)将A(2
,0)代入抛物线解析式可求m的值,得到抛物线解析式,令y=0求x的值,得到B对坐标;
(2)①可根据解析式可得出点C点的在坐标,和函数的对称轴;在Rt△AOC讨论,可得AQ=A′Q,同时,过点A′作A′H⊥x轴,此时可根据两个等量式即可得出QH的长,从而可得出t的值,
②此时要分情况讨论,分当0<t≤1时和当1<t<2时的情况,利用三角函数的知识和四边形求面积的知识即可得出.
| 3 |
(2)①可根据解析式可得出点C点的在坐标,和函数的对称轴;在Rt△AOC讨论,可得AQ=A′Q,同时,过点A′作A′H⊥x轴,此时可根据两个等量式即可得出QH的长,从而可得出t的值,
②此时要分情况讨论,分当0<t≤1时和当1<t<2时的情况,利用三角函数的知识和四边形求面积的知识即可得出.
解答: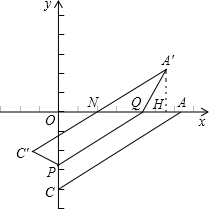 解:(1)将A(2
解:(1)将A(2
,0)代入y=-
mx2+3mx-2,
解得m=
,
∴函数的解析式为y=-
x2+
x-2,
令y=0,解得:x1=
,x2=2
,
∴B(
,0);
(2)①由解析式可得点C(0,-2)
二次函数图象的对称轴为直线x=
,
在Rt△AOC中,∵OC=2,OA=2
,
∴tan∠OAC=
=
,
∴∠OAC=30°,∠OCA=60°,
∴∠PQA=150°,∠A′QH=60°,AQ=A′Q
过点A′作A′H⊥x轴于点H,则QH=AH
∴
,
解得QH=
,
则AQ=
,CP=1
∴t=1,
②分两种情况:
(I)当0<t≤1时,四边形PQA′C′落在第一象限内的图形为等腰三角形QA′N.
NQ=A′Q=
tA′H=A′Qsin60°=
t•
=
tS△A′NQ=
t•
t=
t2,
当t=1时,有最大值S=
.
(II)当1<t<2时,设四边形PQA′C′落在第一象限内的图形为四边形MOQA′,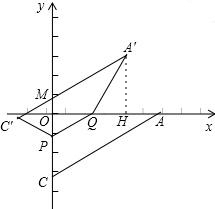
S四边形MOQA′=S梯形PQA'C′-S△OPQ-S△PC'M,
=[2
-
(2-t)2]-
(2-t)2-
t2,
=-
t2+4
t-2
,
当t=
时,有最大值S四边形MOQA′=
,
综上:当t=
时,四边形PQA′C′落在第一象限内的图形面积有最大值是
.
 解:(1)将A(2
解:(1)将A(2| 3 |
| ||
| 3 |
解得m=
| ||
| 3 |
∴函数的解析式为y=-
| 1 |
| 3 |
| 3 |
令y=0,解得:x1=
| 3 |
| 3 |
∴B(
| 3 |
(2)①由解析式可得点C(0,-2)
二次函数图象的对称轴为直线x=
| 3 |
| 2 |
| 3 |
在Rt△AOC中,∵OC=2,OA=2
| 3 |
∴tan∠OAC=
| 2 | ||
2
|
| ||
| 3 |
∴∠OAC=30°,∠OCA=60°,
∴∠PQA=150°,∠A′QH=60°,AQ=A′Q
过点A′作A′H⊥x轴于点H,则QH=AH
∴
|
解得QH=
| ||
| 2 |
则AQ=
| 3 |
∴t=1,
②分两种情况:
(I)当0<t≤1时,四边形PQA′C′落在第一象限内的图形为等腰三角形QA′N.
NQ=A′Q=
| 3 |
| 3 |
| ||
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
| 2 |
3
| ||
| 4 |
当t=1时,有最大值S=
3
| ||
| 4 |
(II)当1<t<2时,设四边形PQA′C′落在第一象限内的图形为四边形MOQA′,

S四边形MOQA′=S梯形PQA'C′-S△OPQ-S△PC'M,
=[2
| 3 |
| ||
| 2 |
| ||
| 2 |
| ||
| 4 |
=-
5
| ||
| 4 |
| 3 |
| 3 |
当t=
| 8 |
| 5 |
| 6 |
| 5 |
| 3 |
综上:当t=
| 8 |
| 5 |
| 6 |
| 5 |
| 3 |
点评:本题是二次函数的综合题型,其中涉及到的知识点有抛物线的顶点公式和三角形的面积求法.在求有关动点问题时要注意分析题意分情况讨论结果.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
已知二次函数y=-x2+bx+c的图象过点A(1,2),B(3,2),C(0,-1),D(2,3).点P(x1,y1),Q(x2,y2)也在该函数的图象上,当0<x1<1,2<x2<3时,y1与y2的大小关系正确的是( )
| A、y1≥y2 | B、y1>y2 | C、y1<y2 | D、y1≤y2 |
 (2013•莒南县二模)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:
(2013•莒南县二模)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论: 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①ac>0;②a-b+c<0;
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①ac>0;②a-b+c<0;