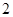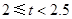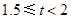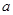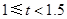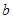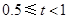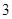题目内容
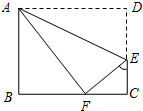 八年级(5)班开展了手工制作竞赛,每个同学都在规定时间内完成一件手工作品.小明月同学在制作手工作品的第一、二个步骤是:①先裁下了一张长BC=20cm,宽AB=16cm的长方形纸片ABCD,②将纸片沿着直线AE折叠,点D恰好落在BC边上的F处,…请你根据①②步骤解答下列问题:
八年级(5)班开展了手工制作竞赛,每个同学都在规定时间内完成一件手工作品.小明月同学在制作手工作品的第一、二个步骤是:①先裁下了一张长BC=20cm,宽AB=16cm的长方形纸片ABCD,②将纸片沿着直线AE折叠,点D恰好落在BC边上的F处,…请你根据①②步骤解答下列问题:(1)找出图中∠FEC的余角;
(2)计算EC的长.
分析:(1)根据折叠的性质得∠AFE=∠D=90°,则∠AFB+∠EFC=90°,而∠BAF+∠AFB=90°,得到∠BAF=∠EFC,由于∠FEC+∠EFC=90°,根据余角的定义得到∠FEC的余角有∠EFC、∠BAF;
(2)根据折叠的性质得AF=AD=20,DE=EF,在Rt△ABF中,根据勾股定理计算出BF=12,则FC=BC-BF=20-12=8,设EC=x,则DE=EF=16-x,在Rt△EFC中,再利用勾股定理得到(16-x)2=x2+82,
解方程即可.
(2)根据折叠的性质得AF=AD=20,DE=EF,在Rt△ABF中,根据勾股定理计算出BF=12,则FC=BC-BF=20-12=8,设EC=x,则DE=EF=16-x,在Rt△EFC中,再利用勾股定理得到(16-x)2=x2+82,
解方程即可.
解答:解:(1)∵长方形纸片ABCD直线AE折叠,点D恰好落在BC边上的F处,
∴∠AFE=∠D=90°,
∴∠AFB+∠EFC=90°,
∵∠BAF+∠AFB=90°,
∴∠BAF=∠EFC,
∵∠FEC+∠EFC=90°,
∴∠FEC的余角有∠EFC、∠BAF;
(2)∵长方形纸片ABCD直线AE折叠,点D恰好落在BC边上的F处,
∴AF=AD=20,DE=EF,
在Rt△ABF中,AF=20,AB=16,
∴BF=
=12,
∴FC=BC-BF=20-12=8,
设EC=x,则DE=EF=16-x,
在Rt△EFC中,
∵EF2=FC2+EC2,
∴(16-x)2=x2+82,
解得x=6,
∴EC的长为6cm.
∴∠AFE=∠D=90°,
∴∠AFB+∠EFC=90°,
∵∠BAF+∠AFB=90°,
∴∠BAF=∠EFC,
∵∠FEC+∠EFC=90°,
∴∠FEC的余角有∠EFC、∠BAF;
(2)∵长方形纸片ABCD直线AE折叠,点D恰好落在BC边上的F处,
∴AF=AD=20,DE=EF,
在Rt△ABF中,AF=20,AB=16,
∴BF=
| 202-162 |
∴FC=BC-BF=20-12=8,
设EC=x,则DE=EF=16-x,
在Rt△EFC中,
∵EF2=FC2+EC2,
∴(16-x)2=x2+82,
解得x=6,
∴EC的长为6cm.
点评:本题考查了折叠的性质:折叠前后两图形全等.也考查了矩形的性质与勾股定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
八年级(1)班开展了为期一周的“孝敬父母,帮做家务”社会活动,并根据学生帮家长做家务的时间来评价学生在活动中的表现,把结果划分成A,B,C,D,E五个等级.老师通过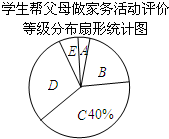 家长调查了全班50名学生在这次活动中帮父母做家务的时间,制作成如下的频数分布表和扇形统计图.
家长调查了全班50名学生在这次活动中帮父母做家务的时间,制作成如下的频数分布表和扇形统计图.
(1)求a,b的值;
(2)根据频数分布表估计该班学生在这次社会活动中帮父母做家务的平均时间;
(3)该班的小明同学这一周帮父母做家务2小时,他认为自己帮父母做家务的时间比班级里一半以上的同学多,你认为小明的判断符合实际吗?请用适当的统计量说明理由.
 家长调查了全班50名学生在这次活动中帮父母做家务的时间,制作成如下的频数分布表和扇形统计图.
家长调查了全班50名学生在这次活动中帮父母做家务的时间,制作成如下的频数分布表和扇形统计图.| 等级 | 帮助父母做家务 时间(小时) |
频数 |
| A | 2.5≤t<3 | 2 |
| B | 2≤t<2.5 | 10 |
| C | 1.5≤t<2 | a |
| D | 1≤t<1.5 | b |
| E | 0.5≤t<1 | 3 |
(2)根据频数分布表估计该班学生在这次社会活动中帮父母做家务的平均时间;
(3)该班的小明同学这一周帮父母做家务2小时,他认为自己帮父母做家务的时间比班级里一半以上的同学多,你认为小明的判断符合实际吗?请用适当的统计量说明理由.
八年级(1)班开展了为期一周的“孝敬父母,帮做家务”社会活动,并根据学生帮家长做家务的时间来评价学生在活动中的表现,把结果划分成 五个等级.老师通过家长调查了全班50名学生在这次活动中帮父母做家务的时间,制作成如下的频数分布表和扇形统计图.
五个等级.老师通过家长调查了全班50名学生在这次活动中帮父母做家务的时间,制作成如下的频数分布表和扇形统计图.
学生帮父母做家务活动时间频数分布表
|
等级 |
帮助父母做家务时间 (小时) |
频数 |
|
A |
|
|
|
B |
|
10 |
|
C |
|
|
|
D |
|
|
|
E |
|
|
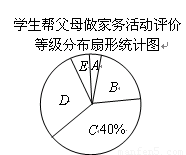
(1)求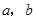 的值;
的值;
(2)根据频数分布表估计该班学生在这次社会活动中帮父母做家务的平均时间;
(3)该班的小明同学这一周帮父母做家务2小时,他认为自己帮父母做家务的时间比班级里一半以上的同学多,你认为小明的判断符合实际吗?请用适当的统计量说明理由.
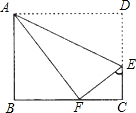 =16cm的矩形纸片ABCD,②将纸片沿着直线AE折叠,点D恰好落在BC边上的F处,…请你根据①②步骤解答下列问题:
=16cm的矩形纸片ABCD,②将纸片沿着直线AE折叠,点D恰好落在BC边上的F处,…请你根据①②步骤解答下列问题: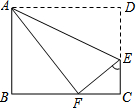 为了向建国六十周年献礼,某校各班都在开展丰富多彩的庆祝活动,八年级(1)班开展了手工制作竞赛,每个同学都在规定时间内完成一件手工作品.陈莉同学在制作手工作品的第一、二个步骤是:
为了向建国六十周年献礼,某校各班都在开展丰富多彩的庆祝活动,八年级(1)班开展了手工制作竞赛,每个同学都在规定时间内完成一件手工作品.陈莉同学在制作手工作品的第一、二个步骤是: