题目内容
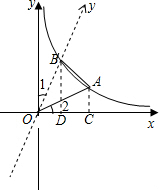
 已知,如图:点A(
已知,如图:点A( ,1)在反比例函数图象上,将y轴绕点O顺时针旋转30°,与反比例函数在第一象限内交于点B,
,1)在反比例函数图象上,将y轴绕点O顺时针旋转30°,与反比例函数在第一象限内交于点B,
求:(1)反比例函数的解析式;
(2)求点B的坐标及△AOB的面积.
 解:(1)设反比例函数的解析式为y=
解:(1)设反比例函数的解析式为y= (k≠0).
(k≠0).∵点A(
 ,1)在反比例函数图象上,
,1)在反比例函数图象上,∴1=
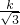 ,
,解得,k=
 ,
,则该反比例函数的解析式是:y=
 ;
;(2)如图,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D.设B(a,b).
∵点A(
 ,1)
,1)∴tan∠22=
 ,
,∴∠2=30°.
又∠1=30°,
∴点A、B关于直线y=x对称,
∴
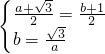 ,
,解得,
 ,则OD=1,BD=
,则OD=1,BD= .
.∴S△AOB=S△OBD+S梯形ABDC-S△AOC=
 OD•BD+
OD•BD+ (AC+BD)•CD-
(AC+BD)•CD- OC•AC=
OC•AC= ×1×
×1× +
+ ×(1+
×(1+ )×(
)×( -1)-
-1)- ×
× ×1=1.
×1=1.综上所述,B点的坐标是(1,
 ),△AOB的面积的面积是1.
),△AOB的面积的面积是1.分析:(1)设反比例函数的解析式为y=
 (k≠0),再把点A(
(k≠0),再把点A( ,1)代入求出k的值,进而可得出反比例函数的解析式;
,1)代入求出k的值,进而可得出反比例函数的解析式;(2)先求出直线OB的解析式,故可得出B点坐标,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D.则S△AOB=S△OBD+S梯形ABDC-S△AOC.
点评:本题考查了坐标与图形的变化--旋转,待定系数法求二次函数解析式.求点B的坐标时,也可以利用一次函数与反比例函数的交点来解答.

练习册系列答案
相关题目
 20、已知:如图,点O为?ABCD的对角线BD的中点,直线EF经过点O,分别交BA、DC的延长线于点E、F,求证:AE=CF.
20、已知:如图,点O为?ABCD的对角线BD的中点,直线EF经过点O,分别交BA、DC的延长线于点E、F,求证:AE=CF. OA上一动点(与点O、A不重合).EF⊥AB于点F,交y轴于点G.设点E的横坐标为x,△BGF的面积为y.
OA上一动点(与点O、A不重合).EF⊥AB于点F,交y轴于点G.设点E的横坐标为x,△BGF的面积为y. 已知:如图,点A、B、C、D在同一条直线上,EA⊥AD,FD⊥AD,AE=DF,AB=DC.BF,CE相交于点O.
已知:如图,点A、B、C、D在同一条直线上,EA⊥AD,FD⊥AD,AE=DF,AB=DC.BF,CE相交于点O.
 (2013•淮阴区模拟)已知:如图,点E、A、C在同一条直线上,AB=CE,AC=CD,BC=ED.求证:AB∥CD.
(2013•淮阴区模拟)已知:如图,点E、A、C在同一条直线上,AB=CE,AC=CD,BC=ED.求证:AB∥CD.