题目内容
观察下列各式:
13=12
13+23=32
13+23+33=62
13+23+33+43=102
…
 猜想 13+23+33+…+103=
猜想 13+23+33+…+103=
552 .
【考点】规律型:数字的变化类.
【专题】规律型.
【分析】13=12
13+23=(1+2)2=32
13+23+33=(1+2+3)2=62
13+23+33+43=(1+2+3+4)2=102
13+23+33+…+103=(1+2+3…+10)2=552.
【解答】解:根据数据可分析出规律为从 1 开始,连续 n 个数的立方和=(1+2+…+n)2 所以 13+23+33+…+103=(1+2+3…+10)2=552.
【点评】本题的规律为:从 1 开始,连续 n 个数的立方和=(1+2+…+n)2.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
个体服装店老板以 32 元的价格购进 30 件连衣裙,针对不同的顾客,30 件连衣裙的售价不完全
相同,若以 47 元为标准,将超过的钱数记为正,不足的钱数记为负,记录结果如下表所示:
| 售出件数 | 7 | 6 | 3 | 4 | 5 | |
| 售价/元 | +3 | +2 | +1 | 0 | ﹣1 | ﹣2 |
该服装店在售完这 30 件连衣裙后,赚了多少钱?
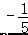 ,则代数式(5a﹣4)(6a﹣7)﹣(3a﹣2)(10a﹣8)的值为( )
,则代数式(5a﹣4)(6a﹣7)﹣(3a﹣2)(10a﹣8)的值为( ) )﹣1+|5﹣
)﹣1+|5﹣ 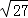 |
|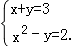
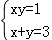 A. B.
A. B. C.
C. 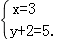 D.
D.