题目内容
用适当的方法解下列方程:
(1)(2x+3)2=x2-6x+9;
(2)3x2+6x-4=0.
解:(1)(2x+3)2=x2-6x+9,
(2x+3)2=(x-3)2,
2x+3=x-3或2x+3=-x+3,
解得:x1=-6,x2=0;
(2)3x2+6x-4=0,
3x2+6x=4,
x2+2x= ,
,
(x+1)2= ,
,
x+1=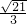 ,
,
解得:x1=-1+ ,x1=-1-
,x1=-1- ;
;
分析:(1)先把原方程变形为(2x+3)2=(x-3)2,得出2x+3=x-3或2x+3=-x+3,再分别解方程即可;
(2)先把常数项-4移到等号的右边,再把二次项系数化为1,然后在等号的两边加上一次项系数一半的平方,用配方法求出方程的解.
点评:此题考查了一元二次方程的解法,用到的知识点是直接开平方法和配方法解方程,解题的关键是掌握直接开平方法和配方法的步骤.
(2x+3)2=(x-3)2,
2x+3=x-3或2x+3=-x+3,
解得:x1=-6,x2=0;
(2)3x2+6x-4=0,
3x2+6x=4,
x2+2x=
 ,
,(x+1)2=
 ,
,x+1=
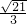 ,
,解得:x1=-1+
 ,x1=-1-
,x1=-1- ;
;分析:(1)先把原方程变形为(2x+3)2=(x-3)2,得出2x+3=x-3或2x+3=-x+3,再分别解方程即可;
(2)先把常数项-4移到等号的右边,再把二次项系数化为1,然后在等号的两边加上一次项系数一半的平方,用配方法求出方程的解.
点评:此题考查了一元二次方程的解法,用到的知识点是直接开平方法和配方法解方程,解题的关键是掌握直接开平方法和配方法的步骤.

练习册系列答案
相关题目