题目内容
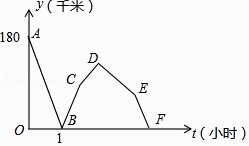
【题目】如图，在Rt△ABC中，∠C=90°，∠B=60°，内切圆O与边AB、BC、CA分别相切于点D、E、F，则∠DEF的度数为°． 
【答案】75
【解析】解：连接DO，FO， 
∵在Rt△ABC中，∠C=90°，∠B=60°
∴∠A=30°，
∵内切圆O与边AB、BC、CA分别相切于点D、E、F，
∴∠ODA=∠OFA=90°，
∴∠DOF=150°，
∴∠DEF的度数为75°．
所以答案是：75．
【考点精析】掌握圆周角定理和三角形的内切圆与内心是解答本题的根本，需要知道顶点在圆心上的角叫做圆心角;顶点在圆周上，且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半；三角形的内切圆的圆心是三角形的三条内角平分线的交点，它叫做三角形的内心．
练习册系列答案
相关题目
【题目】学校开展的“书香校园”活动受到同学们的广泛关注，为了解全校学生课外阅读的情况，随机调查了部分学生在一周内借阅图书的次数，并制成如图不完整的统计图表．
学生借阅图书的次数统计表：
借阅图书的次数 |
|
|
|
|
|
人数 |
|
|
|
|
|
请你根据统计图表中的信息，解答下列问题：
（1）
，
；
（2）该调查统计数据的中位数是 ，众数是 ；
（3）若该校共有
名学生，根据调查结果，估计该校学生在一周内借阅图书
次及以上的人数．
