Question

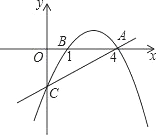
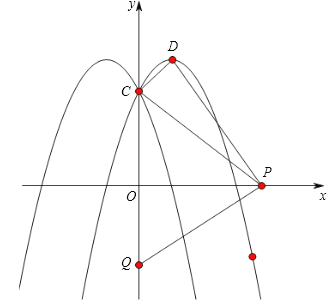
【题目】已知二次函数y=ax2﹣2ax+c（a＜0）的最大值为4，且抛物线过点（，﹣），点P（t，0）是x轴上的动点，抛物线与y轴交点为C，顶点为D．

(1)求该二次函数的解析式，及顶点D的坐标；

(2)求|PC﹣PD|的最大值及对应的点P的坐标；

(3)设Q（0，2t）是y轴上的动点，若线段PQ与函数y=a|x|2﹣2a|x|+c的图象只有一个公共点，求t的取值．

Answer 1

【答案】（1），D（1，4）；（2），P（﹣3，0）；（3）t的取值是≤t＜3或t=或t≤﹣3．

【解析】

试题（1）先利用对称轴公式x=计算对称轴，即顶点坐标为（1，4），再将两点代入列二元一次方程组求出解析式；

（2）根据三角形的三边关系：可知P、C、D三点共线时|PC﹣PD|取得最大值，求出直线CD与x轴的交点坐标，就是此时点P的坐标；

（3）先把函数中的绝对值化去，可知，此函数是两个二次函数的一部分，分三种情况进行计算：①当线段PQ过点（0，3），即点Q与点C重合时，两图象有一个公共点，当线段PQ过点（3，0），即点P与点（3，0）重合时，两函数有两个公共点，写出t的取值；②线段PQ与当函数（x≥0）时有一个公共点时，求t的值；③当线段PQ过点（﹣3，0），即点P与点（﹣3，0）重合时，线段PQ与当函数（x＜0）时也有一个公共点，则当t≤﹣3时，都满足条件；综合以上结论，得出t的取值．

（1）∵的对称轴为：x=1，∴抛物线过（1，4）和（，）两点，代入解析式得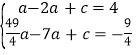：，解得：a=﹣1，c=3，∴二次函数的解析式为：，∴顶点D的坐标为（1，4）；

（2）∵C、D两点的坐标为（0，3）、（1，4）；

由三角形两边之差小于第三边可知：

|PC﹣PD|≤|CD|，∴P、C、D三点共线时|PC﹣PD|取得最大值，此时最大值为，|CD|=，由于CD所在的直线解析式为y=x+3，将P（t，0）代入得t=﹣3，∴此时对应的点P为（﹣3，0）；

（3）的解析式可化为：

设线段PQ所在的直线解析式为y=kx+b，将P（t，0），Q（0，2t）代入得：

线段PQ所在的直线解析式：y=﹣2x+2t，分三种情况讨论：

①当线段PQ过点（0，3），即点Q与点C重合时，线段PQ与函数有一个公共点，此时t=，当线段PQ过点（3，0），即点P与点（3，0）重合时，t=3，此时线段PQ与有两个公共点，所以当≤t＜3时，线段PQ与有一个公共点；

②将y=﹣2x+2t代入（x≥0）得：

，，令△=16﹣4（﹣1）（3﹣2t）=0，t=＞0，所以当t=时，线段PQ与也有一个公共点；

③当线段PQ过点（﹣3，0），即点P与点（﹣3，0）重合时，线段PQ只与（x＜0）有一个公共点，此时t=﹣3，所以当t≤﹣3时，线段PQ与也有一个公共点，综上所述，t的取值是≤t＜3或t=或t≤﹣3．