题目内容
如图，若∠1+∠2+∠3+∠4+∠5+∠6+∠7=n•90°，则n为
- A.4
- B.5
- C.6
- D.7
C
分析：本题就是要求∠1+∠2+∠3+∠4+∠5+∠6+∠7的值，然后结合∠1+∠2+∠3+∠4+∠5+∠6+∠7=n•90°，即可求出答案．
解答：设AG与DE交于点M，与DC交于点N，
则∠5+∠6+∠7=360°-∠ANC，∠2+∠3+∠4=360°-∠EMG，
则∠1+∠2+∠3+∠4+∠5+∠6+∠7=∠1+（360°-∠ANC）+（360°-∠EMG）=720°+∠1-∠ANC-∠EMG=720°+∠1-（180°-∠DMN）-（180°-∠DNM）=360°+（∠1+∠DMN+∠DNM）=360°+180°=540°．
又因∠1+∠2+∠3+∠4+∠5+∠6+∠7=540°=n•90°，
所以n=6．
故选C．
点评：利用三角形以及四边形的内角和定理求出∠1+∠2+∠3+∠4+∠5+∠6+∠7的值是解决本题的关键．
分析：本题就是要求∠1+∠2+∠3+∠4+∠5+∠6+∠7的值，然后结合∠1+∠2+∠3+∠4+∠5+∠6+∠7=n•90°，即可求出答案．
解答：设AG与DE交于点M，与DC交于点N，
则∠5+∠6+∠7=360°-∠ANC，∠2+∠3+∠4=360°-∠EMG，
则∠1+∠2+∠3+∠4+∠5+∠6+∠7=∠1+（360°-∠ANC）+（360°-∠EMG）=720°+∠1-∠ANC-∠EMG=720°+∠1-（180°-∠DMN）-（180°-∠DNM）=360°+（∠1+∠DMN+∠DNM）=360°+180°=540°．
又因∠1+∠2+∠3+∠4+∠5+∠6+∠7=540°=n•90°，
所以n=6．
故选C．
点评：利用三角形以及四边形的内角和定理求出∠1+∠2+∠3+∠4+∠5+∠6+∠7的值是解决本题的关键．
练习册系列答案
相关题目
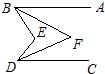如图，若AB∥CD，∠ABE和∠CDE的平分线交于点F，且∠BED=75°，那么∠BFD等于（ ）| A、35° | B、37.5° | C、38.5° | D、36° |
如图，若大圆半径为R，小圆面积是大圆面积的
（1997•重庆）如图．若△ABC的BC边上的高为AH，BC长为30cm，DE∥BC，以DE为直径的半圆与BC切于F，若此半圆的面积是18πcm2，则AH=