题目内容
如图,在平面直角坐标系中,点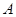 在
在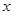 轴上,点
轴上,点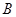 的坐标为(4,2),若四边形
的坐标为(4,2),若四边形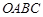 为菱形,则点
为菱形,则点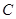 的坐标为 .
的坐标为 .
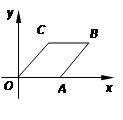
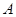 在
在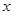 轴上,点
轴上,点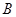 的坐标为(4,2),若四边形
的坐标为(4,2),若四边形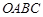 为菱形,则点
为菱形,则点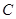 的坐标为 .
的坐标为 .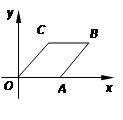
( ,2)
,2)
 ,2)
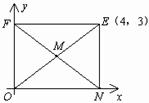
,2)过点B作BD⊥OA于D,并延长BC交y轴与点E,
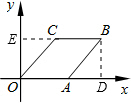
∵四边形ABCD是菱形,∴OC=OA=AB=BC,BC∥OA,设AB=x,则OA=x,AD=4-x,在Rt△ABD中,AB2=AD2+BD2,
即x2=(4-x)2+22,解得:x=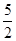 ,∴CE=BE-BC=OD-BC=4-
,∴CE=BE-BC=OD-BC=4-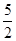 =
= ,∴C点的坐标为(
,∴C点的坐标为( ,2).
,2).

∵四边形ABCD是菱形,∴OC=OA=AB=BC,BC∥OA,设AB=x,则OA=x,AD=4-x,在Rt△ABD中,AB2=AD2+BD2,
即x2=(4-x)2+22,解得:x=
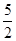 ,∴CE=BE-BC=OD-BC=4-
,∴CE=BE-BC=OD-BC=4-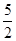 =
= ,∴C点的坐标为(
,∴C点的坐标为( ,2).
,2).
练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
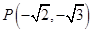 关于
关于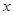 轴对称的对称点的坐标是______________________。
轴对称的对称点的坐标是______________________。
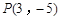 关于x轴对称的点的坐标为( )
关于x轴对称的点的坐标为( )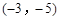
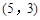
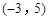
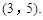
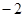 ),在y轴上确定点P,使△AOP为等腰三角形,探究符合条件的点P的个数.
),在y轴上确定点P,使△AOP为等腰三角形,探究符合条件的点P的个数.