Question

【题目】如图Rt中，∠A=30°，OB=2，如果将Rt在坐标平面内，绕原点O按顺时针方向旋转到的位置．

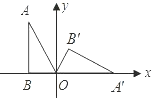
（1）求点的坐标．

（2）求顶点A从开始到点结束经过的路径长．

Answer 1

【答案】（1）B′（1，)；（2）.

【解析】

(1)过点B’作B’D⊥x轴于D

由旋转的性质可知OB’的长,从而求出OD,DB’的长,就可写出B’的坐标
(2)顶点A从开始到A点结束经过的路径长就是一段弧长

由已知题中给出的条件圆心角是120度，半径是0A的长度，然后利用弧长公式计算.

解：（1）过点B′作B′D⊥x轴于D，

由旋转的性质知，∠A′=30°，∠A′OB′=60°，OB′=2，OA′=4，

∴OD=OB′cos60°=2×=1，

DB′=OB′sin60°=2×=，

∴B′的坐标为：B′（1，)．

（2）∵∠AOB=60°，

∴∠AOA′=180°-60°=120°．

∵Rt△ABO中，∠A=30°，OB=2，

∴OA=2OB=4，

∴A由开始到结束所经过的路径长为：=.