题目内容
在△ABC中，AD是角平分线，AE是高，若∠B=50°，∠C=70°，则∠DAE=________．
10°
分析：由三角形内角和定理可求得∠BAC的度数，在Rt△AEC中，可求得∠EAC的度数，AD是角平分线，有∠DAC=
∠BAC，故∠EAD=∠DAC-∠EAC．
解答：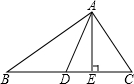
解：∵∠B=50°，∠C=70°，
∴∠BAC=180°-∠B-∠C=60°．
∵AD是角平分线，
∴∠DAC=∠BAC=30°．
∵AE是高，∠C=70°，
∴∠EAC=20°，
∴∠DAE=∠DAC-∠EAC=30°-20°=10°．
点评：本题利用了三角形内角和定理、角的平分线的性质、直角三角形的性质求解．
分析：由三角形内角和定理可求得∠BAC的度数，在Rt△AEC中，可求得∠EAC的度数，AD是角平分线，有∠DAC=
∠BAC，故∠EAD=∠DAC-∠EAC．解答：
解：∵∠B=50°，∠C=70°，∴∠BAC=180°-∠B-∠C=60°．
∵AD是角平分线，
∴∠DAC=
∠BAC=30°．∵AE是高，∠C=70°，
∴∠EAC=20°，
∴∠DAE=∠DAC-∠EAC=30°-20°=10°．
点评：本题利用了三角形内角和定理、角的平分线的性质、直角三角形的性质求解．
练习册系列答案
名校课堂系列答案
相关题目
在△ABC中，AD是高，矩形PQMN的顶点P、N分别在AB、AC上，QM在边BC上．若BC=8cm，AD=6cm，且PN=2PQ，求矩形PQMN的周长．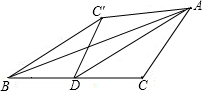
如图，在△ABC中，AD是BC上的中线，BC=4，∠ADC=30°，把△ADC沿AD所在直线翻折后点C落在点C′的位置，那么点D到直线BC′的距离是
（2013•温州二模）如图，在△ABC中，AD是它的角平分线，∠C=90°，E在AB边上，以AE为直径的⊙O交BC于点D，交AC于点F．
如图，在△ABC中，AD是∠BAC的平分线，DE、DF分别是△ABD和△ACD的高线，求证：AD⊥EF．